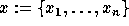 and
and 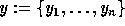 .
One defines for each
.
One defines for each 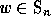 the double Schubert polynomial
the double Schubert polynomial  to
be
to
be



We now consider two independent sets of indeterminates
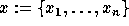 and
and 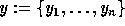 .
One defines for each
.
One defines for each 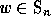 the double Schubert polynomial
the double Schubert polynomial  to
be
to
be
where 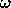 denotes the longest element of
denotes the longest element of 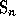 , divided
differences act only on the x variables and
, divided
differences act only on the x variables and

These polynomials which belong to the polynomial ring
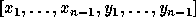 satisfy the following properties:
satisfy the following properties:
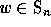 ,
, 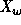 is a non-zero homogeneous polynomial in
is a non-zero homogeneous polynomial in
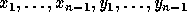 of
degree
of
degree  ,
,
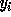 's to 0,
's to 0, 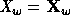 since
since
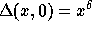 ,
,
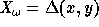 and
and 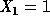 ,
,
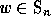 ,
, 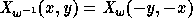 .
.
Double Schubert polynomials generalize the coefficients
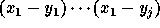 in the Newton interpolation formula (1.10)
to the case of any number of variables. In other words,
considering one set of indeterminates
in the Newton interpolation formula (1.10)
to the case of any number of variables. In other words,
considering one set of indeterminates 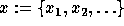 and
and
 denoting any set of elements of a field
denoting any set of elements of a field  ,
the Newton interpolation formula (1.10) becomes
for
,
the Newton interpolation formula (1.10) becomes
for 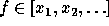 the equation
the equation
in which divided differences act on the y variables.
Thus, working with two sets of variables involves only adding an extra term in Monk's formula (1.38). Furthermore, as in the case of simple Schubert polynomials, one may choose r such that
In the same manner as for the simple Schubert polynomials, it gives a way to
efficiently compute the expression of a double Schubert polynomial in the
basis of monomials but the most interesting point to notice is that it also provides an
efficient way to specialize
(Specialize )
double Schubert polynomials, since in the relation
(1.45) the term 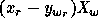 will be very soon specialized to
zero whenever the specialization of the second alphabet to a permutation of the
first one sends the factor
will be very soon specialized to
zero whenever the specialization of the second alphabet to a permutation of the
first one sends the factor  onto zero.
onto zero.
The TableXX function gives the table
of all double Schubert polynomials for 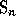 .
.