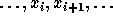 The divided
difference of the function f with respect to the variables
The divided
difference of the function f with respect to the variables 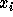 and
and 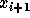 is
is



Consider a function f in the variables 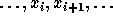 The divided
difference of the function f with respect to the variables
The divided
difference of the function f with respect to the variables 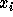 and
and 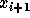 is
is
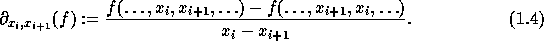
This operator sends polynomials to polynomials and decreases degrees by 1.
The result is a polynomial which is symmetric in 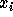 and
and 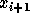 .
.
Consider the polynomial ring 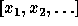 in an infinite
sequence of indeterminates. For each
in an infinite
sequence of indeterminates. For each 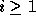 , one can define
, one can define

This operator was introduced by Newton and is called Newton's divided difference. In 1973, Bernstein, Gelfand & Gelfand and Demazure established that divided differences satisfy the braid relations
equation (1.3) being replaced by
Relations (1.6) and (1.7) imply that for any permutation
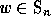 , there exists a divided difference
, there exists a divided difference 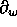 (Newton's case corresponding to elementary transpositions).
If
(Newton's case corresponding to elementary transpositions).
If 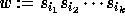 is a reduced decomposition of w, one sets
is a reduced decomposition of w, one sets

Considering a polynomial 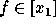 of degree lesser than n
in the unique variable
of degree lesser than n
in the unique variable  and
and 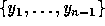 denoting any set of elements of
denoting any set of elements of  , the Newton interpolation formula may be
written
, the Newton interpolation formula may be
written
in which divided differences act on the alphabet
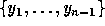 .
The
.
The SP package provides a generalization
of the Newton interpolation formula to polynomials in several variables.
The algebra generated by the  's is called the nilCoxeter algebra
(
's is called the nilCoxeter algebra
(NCA ), or
the algebra of divided differences. It has a linear basis consisting of the
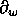 .
.
The user has two types of computations at his disposal: formal computations involving
only the relations (1.6), (1.7), (1.8), or
concrete action on polynomials (NcaOnPol ).
Finally, another basis
(NcaYang )
is given ( Yang-Baxter basis), for which
the braid relations have been replaced by Yang-Baxter equations, e.g.
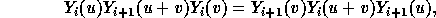
involving extra parameters.