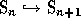Schubert polynomials verify a lot of interesting combinatorial properties related to the symmetric group. They contain as a subfamily Schur functions.
Schubert polynomials are compatible with the embedding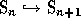 
given by
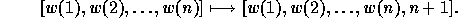
If one identifies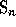 
with its image in 
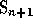, Schubert polynomials
form a basis of the polynomial ring 
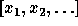in an infinite
sequence of indeterminates.
Algebraic calculation on Schubert polynomials may be described by manipulations of some combinatorial objects (permutations, codes, diagrams, tableaux, ...) or by the use of a scalar product and of self-adjoint operators. This combinatorics includes the combinatorics of Schur functions ---partitions being considered as the Lehmer codes of special permutations, Grassmannian permutations--- and moreover is very similar to it (Pieri's formula, scalar product). Essentially, the combinatorics of partitions (which is the backbone of computations with Schur functions) is replaced by the combinatorics of permutations.
Fix the symmetric group to be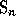 
and let
.
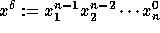For each 
, the (simple) Schubert polynomial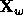 
is defined as
where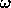 
denotes the longest element (maximal permutation) of 
.
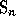Schubert polynomials, for all permutations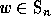 
, are
homogeneous polynomials in 
of degree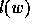 
,
symmetric in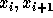 
if and only if the position i is a rise of w.
They verify the following interesting property: let w be a permutation
that factorizes
(FactorPerm )
in a direct product 
.
Then the Schubert polynomial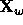 
factorizes too. In other words, whenever
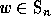belongs to a Young diagonal subgroup 
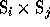so that
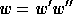, we have also 
.
Schubert polynomials may also be indexed by sequences
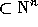interpreted as the code of a permutation
instead of the permutation itself.
We denote by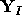 
the Schubert polynomial corresponding to the sequence
. On account of the above properties, one sees
that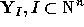 
is homogeneous of degree 
.
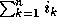The Schubert polynomials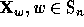 
form a 
basis
(ToX )
of the
subspace of 
spanned by the monomials
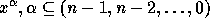, but the crucial fact is
that Schubert polynomials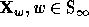 
form a 
basis
of the polynomial ring 
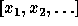in an infinite
sequence of indeterminates.
The Schubert polynomials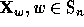 
form a basis for the
algebra of polynomials 
as a module over the ring of
symmetric polynomials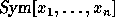 
. The multiplicative structure
in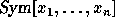 
is determined by Pieri's formula that expresses
in the basis of Schur functions the product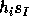 
(resp. 
), 
,
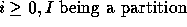where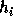 
(respectively 
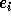) denotes the i-th complete
(respectively elementary) symmetric function.
In the Schubert basis, the multiplicative structure is based on
the multiplication by one variable
(Monk ).
It involves a certain combinatorics on
permutations that is described by Monk's formula:
where 
denotes the transposition that interchanges
i and j.
For the time being, Monk's formula appears as the
fundamental tool for calculation on Schubert polynomials. For instance, one may
choose r such that only one positive term appears in the product
. This provides a way to develop a Schubert polynomial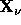 
on the basis of monomials
(X2x )
since we have
The TableX function gives the table
of all Schubert polynomials for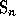 
.
In relation with the cohomology ring of flag manifolds, it is natural to define
a scalar product on 
for which elements of the ring
of symmetric polynomials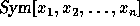 
are scalars. The use
of the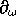 
operator seems to be the best adapted
so that one defines the scalar product (corresponding to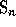 
) as
that is (in the basis of Schur functions) the symmetric function
obtained by applying the maximal divided difference
(ScalarSf )
of 
to the product
fg.
