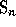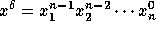Schubert polynomials were introduced in 1982 by Lascoux and Schützenberger
as a combinatorial tool for certain questions of algebraic
geometry. Given a symmetric group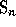 
, they are the images by divided
differences of the monomial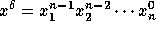 
.
They are polynomials in n variables, indexed by permutations 
---since divided differences are so---, which provide a convenient basis of the
polynomial ring regarded as a free module of dimension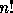 
on the ring of symmetric polynomials.
They are non-negative integral linear combinations of the monomials of the
obvious basis
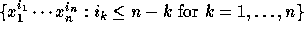, over which
they present many advantages.