La donnée géoréférencée dispose de plusieurs dimensions. En revanche le support de stockage de l'index lui n'en dispose que d'une seule. Que l'index soit stocker en ram ou non il s'agit de représenter une structure en 2 dimensions minimum sur une seule. Etant donné les temps d'accès de certains support tel que les disques durs. Il est nécessaire de garder les données proches géographiquement et sur le disque dur pour garder des performances optimale.

Une courbe parcourant l'ensemble de l'espace de façon prévisible et ordonnée serait l'idéale pour pouvoir projeter nos données multi-dimensionnel sur une seule dimension. Un élément de réponse est apporté par les fractales. Ces courbes sont identiques qu'importe l'échelle à laquelle on les regardes. Il nous suffirait de suivre cette courbe pour ensuite écrire les valeurs dans l'ordre.
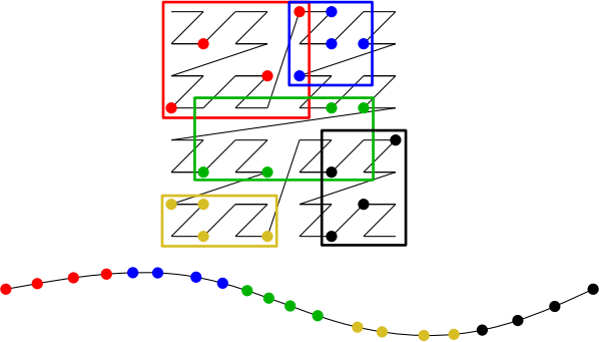
La Z-Curve parcourt l'espace en formant un Z. Elle répond à notre problématique en parcourant les éléments proches de façon linéaire. Elle peut parcourir les espaces en 2 et 3 dimensions et est souvent utilisée dans les implémentations des quadtrees.
Les extensions spatiales des bases de données Oracle et SQLServer utilise la Z-Curve pour créer leur index spatiaux.
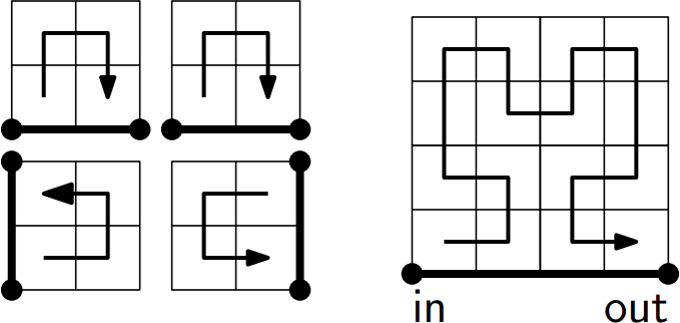
La courbe d'Hilbert est similaire à la courbe en Z et produit un résultat similaire. Elle offre cependant une meilleure répartition dans l'espace. Cette courbe garde les éléments plus proche que la Z-Curve. La courbe d'Hilbert est cependant plus complexe.
La complexité de la courbe n'est par le seul élément négatif. Il est possible, avec une courbe d'Hilbert, de parcourir l'espace de plusieurs façon différentes. Il est indispensable de connaître l'ordre de parcourt pour assurer l'interopérabilité en deux parcours d'Hilbert.
Il existe une structure de données nommé Hilbert R-Tree et réunissant les avantages de la courbe d'Hilbert avec ceux des R-Tree.