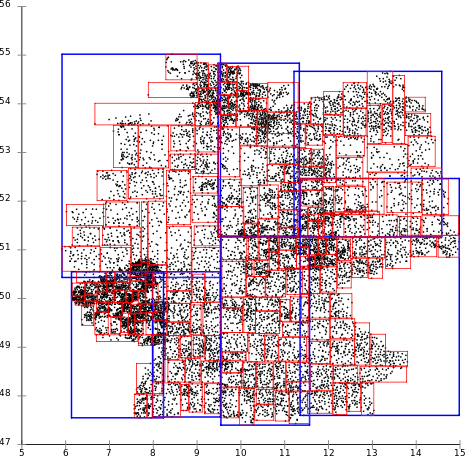
La grille est l'index spatial le plus connu car présent sur la plupart des cartes. Facile à implémenter et utiliser, la grille souffre cependant d'inconvénients difficile à outrepasser.
Tout d'abord on peut utiliser plusieurs formes pour créer une grille sur la zone à indexer :
- Le triangle : la plus petite géométrie pour représenter un plan, cette permet souvent de simplifier les algorithmes et est apprécier des GPU. Elle va demander un découpage complexe de la zone.
- Le rectangle : le rectangle et le plus connu car visible sur les cartes, en revanche il est difficilement applicable sur une sphère et se retrouve donc déformé lors d'un affichage à l'écran.
- L'hexagone : une géométrie qui s'adapte bien aux sphère et à leur coordonnées sphériques (souvent connu du grand public à travers les coordonnées GPS). Les algorithmes nécessaire à son implémentation sont plus complexes que ceux nécessaires pour un triangle ou un rectangle.
Si la géométrie à utiliser est problématique, le plus gros problème vient de l'adaptation de la grille. Une grille quadrillant l'ensemble de la terre mais indexant des données françaises sera souvent inutile car les cellules de la grille seront trop grandes.
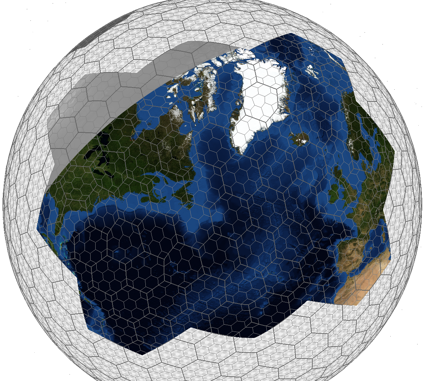
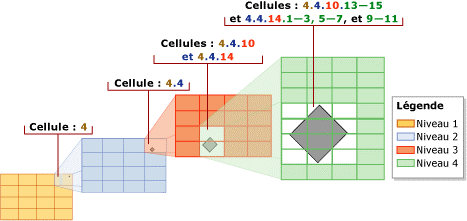
Une structure de donnée pourrait contenir une grille dans une grille. On règlerait ainsi le problème des grilles non adaptés. Au prix d'une complexité légèrement accrue, la grille deviendrait récursive et chaque cellule d'une grille pourrait contenir une autre grille. Il faut alors se poser du nombre de niveau dans la grille. Quand arrêter la récursion?
La taille des cellules d'une grille est difficile à définir, un index sur les départements n'a pas besoin d'une grille aussi dense qu'un index sur les bâtiments. La structure, pour présenter des performances optimale devront être configurer pour chacune des données sur lesquelles on créé un index. Une situation difficilement concevable pour l'informaticien moyen.
Enfin pour savoir si une géométries doit être référencé dans une grille spécifique il faut effectuer une opération de tesselation sur la géométries avec les cellules. La tesselation est une opération couteuse qui affaiblit grandement les performances de l'index.
Les quadtrees sont une structure de donnée permettant d'indexer des géométries en deux dimensions. Plutôt simple à implémenter pour de la donnée ponctuelles ils demandent une réflexion un peu plus poussée pour indexer des polygones et des lignes.
Un quadtree subdivise successivement l'espace en 4 parties égales. Cette structure est un arbre et demande une hauteur maximum pour ne pas que la subdivision se poursuive à l'infini. Chaque noeud de l'arbre représentant une zone il suffit de vérifier si la zone correspond à la zone recherchée. Si la réponse est positive on descend dans la branche sinon on arrête. La racine de l'arbre correspond à l'ensemble de l'espace.
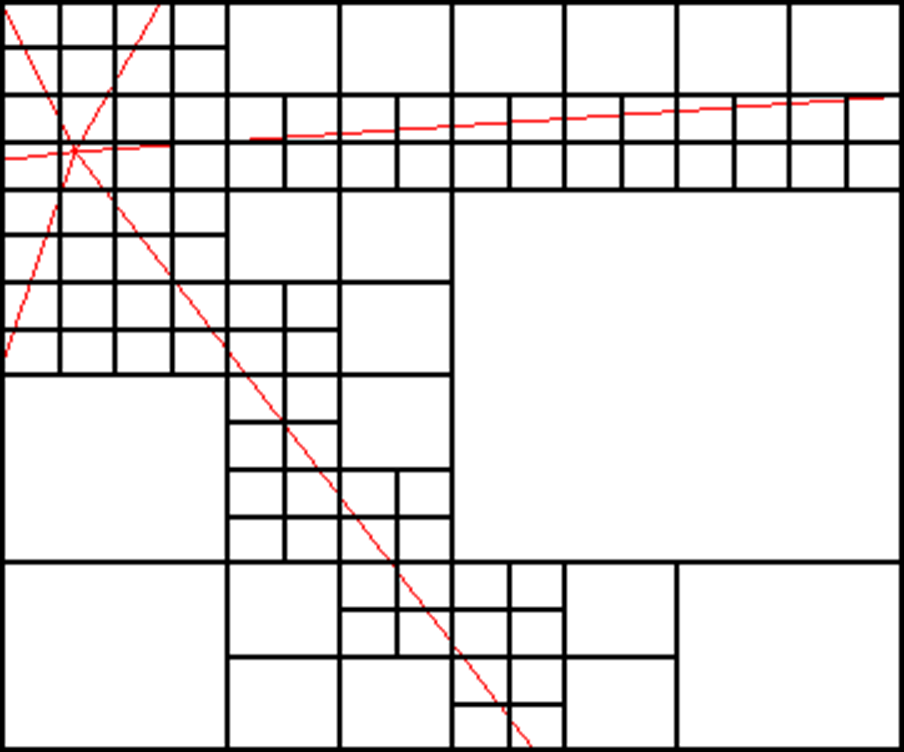
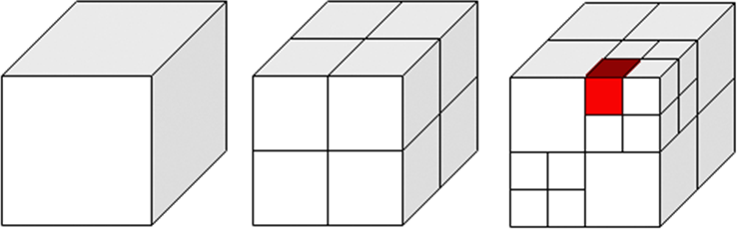
Les octrees sont les descendants directes du quadtree. Ils permettent d'indexer tout les types de géométries et en 3 dimensions. L'espace est divisé en son centre en 8 parties égales.
La structure de donnée de l'octree est très souvent utilisée en 3D et notamment pour implémenter le frustum culling. Le frustum culling permettre de ne faire dessiner au GPU que les objects 3D qui intersectent le champ de visiion de la caméra.
Tout comme les quadtree ils demandent à définir une hauteur maximum à l'arbre.
Pour les quadtrees on divise l'espace en 4, pour les octrees en 8, donc pour k dimensions il suffirait de diviser en 2^k pour avoir une structure correcte. Cette approche amènerai à créer de nombreux noeuds inutilement.
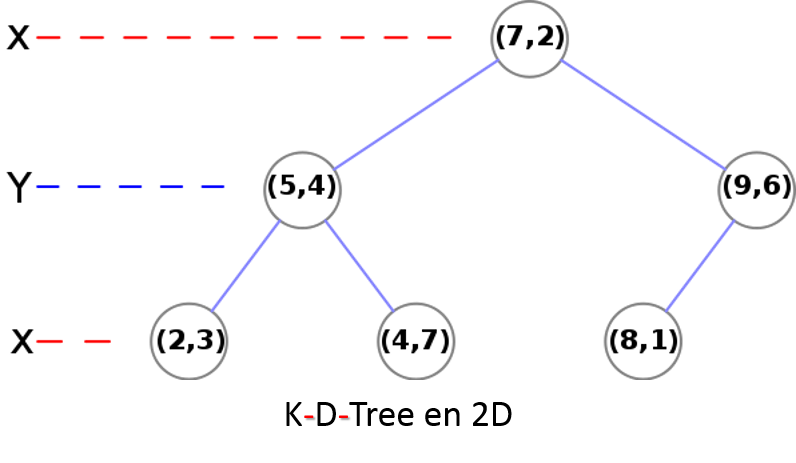
Une solution différente à été donnée via les K-D-Tree (D pour dimensionnel). Les K-D-Tree sont des arbres binaires où chaque niveau de l'arbre correspond à une dimension sélectionnée de façon cyclique. Pour placer notre élément dans l'arbre on compare la valeur de la dimension du niveau du noeud avec la donnée à insérer.
Outre le fait que la structure soit très simple à mettre en place, elle permet d'indexer des géométries en k dimensions. Chaque dimensions est couper en deux et la taille de l'arbre dépend du nombre de points à insérer.
Cette structure demande de grosses modifications pour stocker des polygones et des lignes et est donc peu adaptée pour de la donnée réelle.
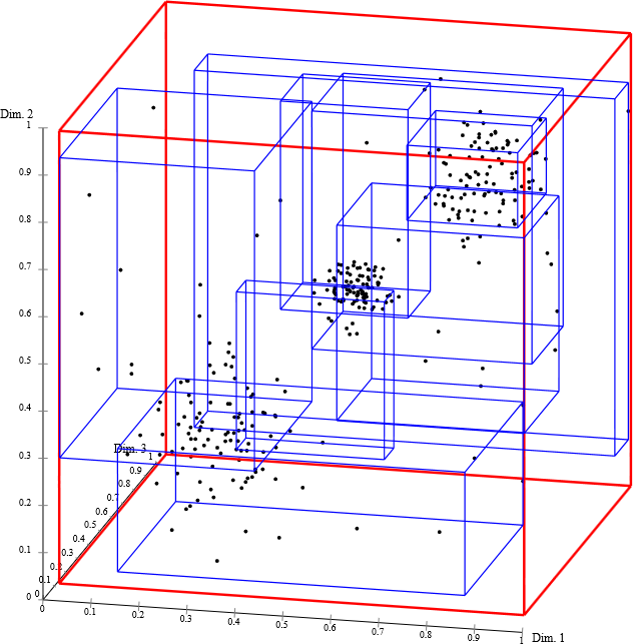
Toutes les structures vues précédemment imposent des contraintes fortes sur la donnée ou sur la configuration de la structure. Une solution plus complexe mais résolvant la plupart des problèmes soulevés par les autres structures existe, les R-Tree. Un R-Tree peut stocker des données en 2D ou 3D. Cet arbre se base sur les Binary Search Tree. Les noeuds de l'arbres représente la Bounding Box (polygone englobant) des géométries qu'il contient.
Les bounding boxes facilitent grandement les opérations d'inclusion ou d'intersection. La création des bounding boxes est cependant primordial. De mauvaises bounding peuvent pénaliser les performances de l'index.
Certaines géométries peuvent être présentes dans plusieurs noeuds de l'arbre. Ce phénomène doit être évité au maximum pour que l'index soit performant.
Outre le fait que la structure soit très simple à mettre en place, elle permet d'indexer des géométries en k dimensions. Chaque dimensions est couper en deux et la taille de l'arbre dépend du nombre de points à insérer.
L'implémentation des R-Tree, rbush, réalisée par le créateur de Leaflet, mourner, permet d'intéragir avec un R-Tree depuis une page web. Jouez avec un R-Tree!
La création des bounding boxes est une étape primordiale dans la création d'un R-Tree et est souvent l'étape la plus couteuse. Les R*Tree propose un découpage topologique de l'espace, limitant ainsi le chevauchement des bouding boxes mais également une extension trop importante des bounding boxes.
Le découpage topologique de la zone reste complexe à mettre en oeuvre et certains R-Tree choisissent de ne pas l'implémenter. A cause de ce découpage l'insertion dans un R*Tree à une complexité en O(n log n). La réinsertion en revanche à une complexité en O(log n).
Une optimisation classique des R*Tree est de mettre en place un système de bulk loading (chargement en gros) qui va insérer l'ensemble des données à un endroit non optimale avant de les réinsérer. Le temps de construction totale sera ainsi réduit pour accélérer la construction.