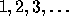 without repetition.
without repetition.



They are two dimensional arrays
obtained by filling the Ferrers diagram of a partition
with numbers, in such a way that numbers are weakly increasing
in rows from left to right, and strictly increasing
from bottom to top. A tableau is standard if the numbers
used are 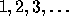 without repetition.
without repetition.
Tableaux also code linear bases of irreducible representations of the symmetric and linear groups.
We represent tableaux by the sequence of its rows:

will be coded in the package by Tab:=[ [3,5] ,[2,4], [1,1,3] ].
We recover from it the planar tableau using the
Tab2Mat function .
A tableau can be considered as the word
(Tab2Word )
obtained by concatenating its rows.
From this word, one reconstructs without ambiguity
the tableau by cutting the word at each decrease.
More generally, Schensted has described an algorithm
(a ``bumping process'') to
transform any word into a tableau: if Tab is the tableau
obtained by this algorithm from the word w,
then the tableau corresponding to the word wx is
obtained by
Bump(Tab, x);
Two words which give the same tableau are said to be plactically equivalent. As shown by Knuth, this equivalence on words is induced from the following equivalence on words of length 3 (i<j<k):
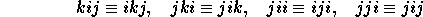
By pushing, thanks to the ``jeu de taquin'', a planar tableau into
a north-east corner, one gets a contretableau
which will be coded by the sequence of its columns, from left to right,
each column being read from top to bottom.
The system provides the functions
CTab2Word ,
CTab2Mat , ...,
which are exactly the analogues of the functions for tableaux.
There is also an algorithm to get from any word a contretableau
(Word2CTab ),
the elementary step being given by BumpC .
Another way of coding standard tableaux is by Yamanouchi words,
i.e. words w such that for each factorisation
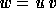 , then
, then 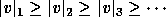 ,
where
,
where 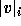 denote the number of times the letter i appears
in v.
This coding just tells in which rows in the standard tableau are the
letters
denote the number of times the letter i appears
in v.
This coding just tells in which rows in the standard tableau are the
letters 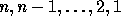 .
One has the inverse function, from Yamanouchi words to standard tableaux
.
One has the inverse function, from Yamanouchi words to standard tableaux
Yama2StdTab .
The shape of a tableau is the list of the lengths of its successive
rows, and thus is a partition which is given by the function
Tab2Part .
Given a partition, the function
Part2ListStdTab
enumerates all the standard tableaux of shape this partition.
The equivalent enumeration of
Yamanouchi words is given by ListYama .
A tableau t gives a word in non commuting letters 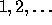 ,
but also a monomial
,
but also a monomial 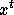 by replacing each letter i by the
variable
by replacing each letter i by the
variable 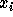 . Now, through this transformation,
the sum of all tableaux of a given shape part gives a polynomial
. Now, through this transformation,
the sum of all tableaux of a given shape part gives a polynomial
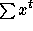 which is exactly the Schur function of index
the partition conjugate to part. The best way to explain why the sum
of all tableaux give a symmetric function is to introduce an action
of the symmetric group on words, which sends tableaux to tableaux
of the same shape, and is compatible with plactic equivalence.
This action is given by the
which is exactly the Schur function of index
the partition conjugate to part. The best way to explain why the sum
of all tableaux give a symmetric function is to introduce an action
of the symmetric group on words, which sends tableaux to tableaux
of the same shape, and is compatible with plactic equivalence.
This action is given by the PermOnWord
function .
Now, the set of tableaux of a given shape is globally invariant under
this action. Of course, the induced action on the monomials
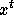 is the usual action of the symmetric group on the
variables
is the usual action of the symmetric group on the
variables 
Finally, to each word one associates two integral vectors,
its charge vector
(that can be computed by the Word2Charge
function )
and its cocharge vector
(Word2CoCharge ).
These two vectors are compatible with Schensted algorithm and the plactic equivalence, as well as with cyclic permutations on words. The sum of the entries in the cocharge vector is a number which is the height of the tableau, when the set of all tableaux is made a rank poset by the operation of deleting the first letter of a tableau and inserting from the right:
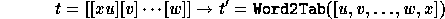
On the other hand, the sum 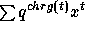 on all tableaux
of a given shape part, where
on all tableaux
of a given shape part, where 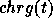 is the sum of the entries
of the charge vector, is the Hall-Littlewood polynomial
is the sum of the entries
of the charge vector, is the Hall-Littlewood polynomial
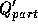 .
.


