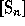 (
(SGA )
in which  stands for any ring
of coefficients is defined as the algebra
generated by the elementary transpositions
stands for any ring
of coefficients is defined as the algebra
generated by the elementary transpositions 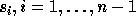 .
Thus it has a natural linear basis consisting of all
permutations in
.
Thus it has a natural linear basis consisting of all
permutations in 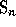 .
.



The symmetric group algebra 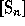 (
(SGA )
in which  stands for any ring
of coefficients is defined as the algebra
generated by the elementary transpositions
stands for any ring
of coefficients is defined as the algebra
generated by the elementary transpositions 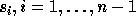 .
Thus it has a natural linear basis consisting of all
permutations in
.
Thus it has a natural linear basis consisting of all
permutations in 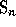 .
.
We give special elements, which are called
Jucis- Murphy elements:
Jucis(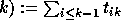 , sum on all transpositions
exchanging i and k,
, sum on all transpositions
exchanging i and k, 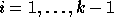 .
.
The algebra generated by the Jucis-Murphy elements is a maximal commutative
sub-algebra of the symmetric group algebra. The symmetric functions in these
elements span the center of the group algebra 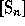 .
.
Using these elements, one can build central idempotents corresponding to standard
tableaux, which are mutually orthogonal
(StdTab2Idemp ).
Carre(perm) and
Nabla(perm) ) are other distinguished
linear bases of 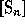 . One can obtain idempotents from them:
. One can obtain idempotents from them:
Carre[LastPerm(n)] is the sum of all permutations in 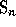 and
and
Nabla[LastPerm(n)] is the alternated sum of all permutations in
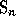 .
More generally, corresponding to a given shape, e.g.
.
More generally, corresponding to a given shape, e.g. 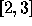 , one will have the
idempotent
, one will have the
idempotent Carre([2,4,1,3,5]) 

Nabla([2,5,1,4,3])
that one gets from reading the following special tableaux and contretableaux:
