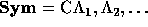 generated by
an infinite sequence of noncommuting indeterminates
generated by
an infinite sequence of noncommuting indeterminates 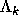 , called
the elementary functions. It is convenient to set
, called
the elementary functions. It is convenient to set 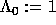 .
Let t be another indeterminate, commuting with the
.
Let t be another indeterminate, commuting with the 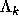 . One
introduces the generating series
. One
introduces the generating series



Recently, starting from the quasi-determinants of Gelfand and Retakh [,] a noncommutative theory of symmetric functions has been developed [], in such a way that most of the classical applications can be lifted to the noncommutative case. In particular, the character theory of the symmetric group has a natural noncommutative analogue, in which the rôle of the character ring is played by Solomon's descent algebra [].
The algebra of formal
noncommutative symmetric functions is the free associative
algebra 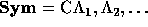 generated by
an infinite sequence of noncommuting indeterminates
generated by
an infinite sequence of noncommuting indeterminates 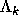 , called
the elementary functions. It is convenient to set
, called
the elementary functions. It is convenient to set 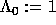 .
Let t be another indeterminate, commuting with the
.
Let t be another indeterminate, commuting with the 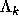 . One
introduces the generating series
. One
introduces the generating series
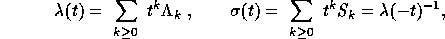
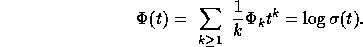
The  are called complete symmetric functions, and the
are called complete symmetric functions, and the 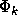 are
the power sums of the second kind. The power sums of the first kind,
denoted by
are
the power sums of the second kind. The power sums of the first kind,
denoted by 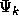 are the coefficients of the formal series
are the coefficients of the formal series
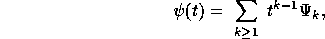
defined by the equation
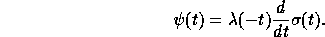
The algebra 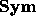 is graded by the weight function w defined by
is graded by the weight function w defined by
 , and its homogeneous component of weight n is denoted
by
, and its homogeneous component of weight n is denoted
by 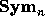 . If
. If 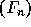 is a sequence of noncommutative symmetric functions
such that
is a sequence of noncommutative symmetric functions
such that 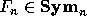 , we set for any composition
, we set for any composition 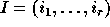

Then, 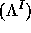 ,
,  ,
, 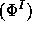 and
and 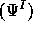 are homogeneous bases of
are homogeneous bases of 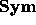 (
(ToL ,
ToS ,
ToPh ,
ToPs ).
The set of all compositions
(ListCompo )
of a given integer n is equipped with
the reverse refinement order
(ListCompoFiner ,
IsFiner ),
denoted 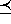 . For example,
the compositions J of 5 such that
. For example,
the compositions J of 5 such that 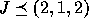 are
are  ,
,
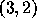 ,
,  and
and 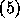 . The basis
. The basis 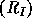 of ribbon Schur functions,
originally defined in terms of quasi-determinants in [], can
also be defined by either of the two equivalent equations
of ribbon Schur functions,
originally defined in terms of quasi-determinants in [], can
also be defined by either of the two equivalent equations
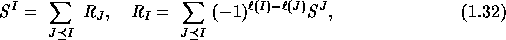
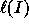 being the length of the composition I
(
being the length of the composition I
(ToR ).
The commutative image of a noncommutative symmetric function
is given by the algebra morphism  .
Then,
.
Then, 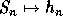 ,
, 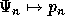 ,
, 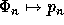 ,
and
,
and 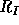 is sent to an ordinary ribbon Schur function, which is
denoted by
is sent to an ordinary ribbon Schur function, which is
denoted by 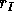 . Ribbon Schur functions have been defined by
McMahon ( see [], t. 1, p. 200), and are denoted in his book by
. Ribbon Schur functions have been defined by
McMahon ( see [], t. 1, p. 200), and are denoted in his book by 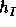 .
.
Let 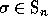 be a permutation with descent set
be a permutation with descent set
 .
The descent composition
(
.
The descent composition
(Perm2Desc )
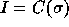 is the composition
is the composition 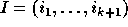 of n defined by
of n defined by
 , where
, where 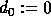 and
and 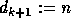 . We
also set
. We
also set 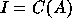 , and conversely, the subset
A of
, and conversely, the subset
A of 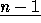 associated to a composition I of n
is denoted by
associated to a composition I of n
is denoted by 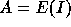 .
The sum in the group algebra
of all permutations with descent composition I is denoted by
.
The sum in the group algebra
of all permutations with descent composition I is denoted by 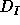 . The
. The
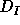 with |I|=n form a basis of a subalgebra
with |I|=n form a basis of a subalgebra 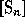 , called the
descent algebra of
, called the
descent algebra of 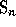 []. We denote by
[]. We denote by 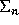 the same algebra, with scalars extended to
the same algebra, with scalars extended to  . There is
an isomorphism of graded vector spaces
. There is
an isomorphism of graded vector spaces
such that

for any composition I.
The direct sum 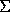 can be given an algebra structure, by extending the
natural product of its components
can be given an algebra structure, by extending the
natural product of its components 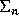 by setting xy=0 for
by setting xy=0 for
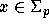 and
and 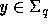 with
with 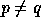 . The
internal product
(
. The
internal product
(Internal ),
denoted  , on
, on 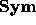 is defined by requiring that
is defined by requiring that  be an anti-isomorphism. That is, we set
be an anti-isomorphism. That is, we set
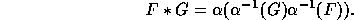
One also defines on 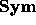 a coproduct
a coproduct 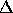 by any of the following
equivalent conditions:
by any of the following
equivalent conditions:
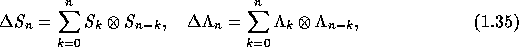
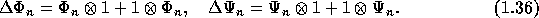
The fundamental property for computing with the internal product is the following splitting formula:
In the commutative case, this formula can be regarded as a particular case of the Mackey tensor product theorem.
With this coproduct, the involution 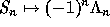 ,
and the natural unit and counit,
,
and the natural unit and counit, 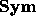 is a Hopf algebra,
whose graded dual is Gessel's algebra of quasisymmetric functions
[].
is a Hopf algebra,
whose graded dual is Gessel's algebra of quasisymmetric functions
[].
It has been shown by Klyachko [] that for a primitive
n-th root of unity  , the element
, the element
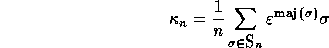
is a Lie idempotent. In terms of noncommutative symmetric functions,
this element is the specialization at 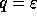 of the
symmetric function
of the
symmetric function 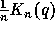 , where
, where 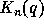 is given by the
generating series
is given by the
generating series
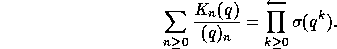
The symmetric functions of the virtual alphabet
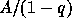 (
(SpDirect )
are defined by the equation

where A is just a label.
The inverse transformation is given by the function SpInverse.
For example, 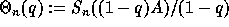 corresponds in the
descent algebra to the q-bracket operator.
corresponds in the
descent algebra to the q-bracket operator.
As an application, one can show that the element

is a Lie idempotent [,], interpolating between several known ones.
As shown in [], this leads to a q-deformation of the Eulerian idempotents.


