Algorithmes de Résolution des SUDOKUS
Le Sudoku
Principe du Sudoku
L' Origine du jeu:
Le Sudoku est un jeu sous forme de grille inspiré du carré latin et défini en 1979 par Howard Garns.
Il est publié pour la première fois en 1984 par Kaji Maki dans une revue mensuelle sous le nom de "Suji wa dokushin ni kagiru" ce qui signifie "Chiffre limité à un seul".

Règles du jeu:
Le sudoku est une grille carrée divisée en n² région de n² cases et possède n² colonnes, n² lignes et n²*n² cases.
La seule régle à respecter est: dans chaque ligne, chaque colonne, chaque région, les chiffres de 1 à n² apparaissent une et une seule fois. Cette régle se traduit aussi par : chaque ligne, chaque colonne et chaque région doit contenir au moins une fois tous les chiffres de 1 à n²
Dans la version courante n=3.Variantes:
Il existe différentes variantes du sudoku. Exemple : le triple X, le Samouraï

Visualisation sous forme de graph
Définition:
On peut visualiser une grille de sudoku sous la forme d'un graph. Les cases sont représentées par des noeuds colorés en fonction de leur contenu.
Chaque chiffre de 1 à n² est representé par une couleur. Tous les noeuds appartenant à une même région, ligne ou colonne sont reliés par une arrête, et une grille est remplie correctement lorsqu'aucun des deux noeuds reliés n'ont la même couleur.
Exemples
Voici un exemple concret d'une reprétation d'une grille de sudoku sous la forme d'un graph. Cette grille est une grille n=2, chaque chiffre 1, 2, 3 et 4 est associé à une couleur et chaque case est représentée par un noeud et est associé aux noeuds correspondant aux cases figurant sur sa ligne, sa colonne ou dans sa ré.
Pour des raisons de lisibilité seule les arrètes du noeud 1 ont été représentées.

Sudoku à solution unique
Quelques chiffres
Le nombre de grille complètes possibles est de 6,67.10^21.
Si l'on considère que deux grilles sont identiques lorque l'on peut arriver de l'une à l'autre par des opérations matricielle alors le nombre de grilles différentes est de 5 472 730 538.
Symétries des grilles
Voici une liste de différentes operations matricielles que l'on peut effectuer sur une grille et qui préservera sa validité.
Permutation des lignes de même blocs de ligne:

Permutation des colonnes de même blocs de colonne:

Permutation des chiffres:
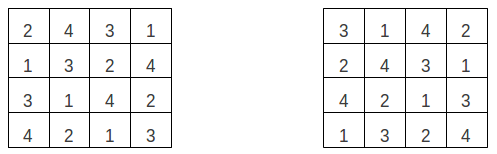
Rotation de la matrice:
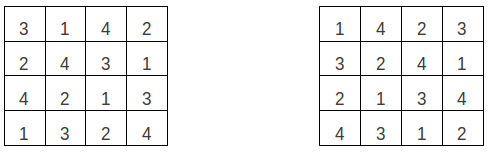
Permutation de blocs de ligne: