Une fois la matrice de similarité calculée, il est possible de classer automatiquement les documents. Comme annoncé, plusieurs techniques existent. Certaines sont dites hiérarchiques (HAC) car elles produisent une hiérarchie, alors que d’autres sont dites non hiérarchiques (single-pass, SOM). D’autres encore produisent des classes floues (STC et Bayesian).

Single-Pass [hill 68]

Une première méthode traite les documents séquentiellement : on met le premier document dans un cluster.

On regarde sa similarité avec le second document. Si elle est supérieure à un seuil fixé par l’usager, alors on range le second document dans le cluster (qui ne contenait que le premier document). On continue avec le troisième document, et ainsi de suite tant que la similarité entre le cluster défini et le document actuel dépasse le seuil. La similarité entre le cluster et un document est la moyenne des similarité entre chaque document du cluster et le document.

Quand le seuil n’est pas dépassé, alors on obtient un cluster et une liste de documents non traités. On recommence au début en définissant un nouveau cluster qui contient le premier document de la liste de documents non traités. 

Cette première méthode a un inconvénient : elle traite les documents séquentiellement. C’est à dire que les résultats de la classification dépend de l’ordre de traitement des documents ! Mais elle est aussi un avantage en termes de rapidité ! Néanmoins, il serait préférable de chercher le document le plus similaire au cluster courant dans la liste des documents non encore traités. C’est la seconde méthode (“ best-first iterative partitioning ”): on cherche les deux documents les plus similaires : on les range dans le cluster 1. Tant qu’on trouve un document dont la similarité avec le cluster 1 dépasse un seuil fixé, on ajoute ce document au cluster 1. Quand on n’y arrive plus, on forme le cluster 2 contenant les deux documents les plus similaires parmi ceux pas encore traités. On continue jusqu’à ce que tous les documents aient été traités.

K-mean [Rocchio 66]

On doit définir à l’avance le nombre de clusters à obtenir.

On répartit ces clusters en les représentant par un vecteur, comme les documents à classer.

Ensuite, on ajoute à chaque cluster le document qui lui est proche. On recalcule le vecteur de ce cluster (moyenne entre le vecteur du cluster et du nouveau document rajouté). On continue ce processus tant qu’il reste des documents à classer.

Avantage : un document peut être rangé dans plusieurs clusters.

L’inconvénient de cette méthode est qu’on doit spécifier à l’avance le nombre de clusters. De plus, le choix des clusters de départ semble important.

Par contre, cette méthode est rapide : O(nK) avec n le nombre de documents et K le nombre de clusters désirés.

Hierarchical Agglomerative Clustering [Voorhees 86]

Mais cette seconde méthode ne produit pas de hiérarchies. La plupart des méthodes de classification de documents sont au contraire des méthodes dites “ hierarchical agglomerative clustering ” (HAC). En effet, la méthode 2 ne peut regrouper qu’un cluster et un document, et non pas un cluster et un autre cluster. La troisième méthode est donc la suivante : on range au départ chaque document dans un cluster. Ensuite on cherche les deux clusters les plus proches. On les fusionne pour former un nouveau cluster et on répète tant qu’il reste au moins deux clusters.

Il existe plusieurs versions de cette méthode standard HAC (single linkage, group average linkage, complete linkage). Seul le calcul de la similarité entre deux clusters change :

pour single linkage, Similarité = Similarité maximum entre un document de cluster1 et un document de cluster2.
pour group average linkage, Similarité = moyenne des similarités entre les documents de cluster1 et cluster2.
pour complete linkage, Similarité = Similarité Minimum entre un document de cluster1 et de cluster2

 On peut aussi diviser la valeur de la similarité par le nombre de documents présents dans le cluster : cela évite de produire des clusters contenant trop de documents.

Ces trois méthodes ont des temps d’exécution allant de O(n²) (Single-link et group average) à O(n3) pour complete-link.  Les méthodes single-link et group-average  ont tendance à générer des gros clusters. L’inconvénient de group-average est en plus de générer des vecteurs très grands pour chaque cluster (puisqu’on fait à chaque fois la moyenne des documents présents dans le cluster : peu à peu il ne reste presque plus de 0 dans le vecteur !). Mais group-average reste malgré tout le plus utilisé car il représente un bon compromis entre vitesse de calcul et qualité des clusters générés.

Les méthodes HAC, bien que très populaires, restent toutefois lentes. De plus, elles ne fonctionnent pas bien sur peu de mots. Ce peut être le cas lorsqu’on cherche à classer automatiquement non pas des documents entiers, mais des résumés de documents (retournés par exemple par les moteurs de recherche comme Altavista) ou quand on veut classer les documents à partir des mots surlignés dans un logiciel d’annotation.

Buckshot anf Fractionation [Cutting 92]

Buckshot est une version modifiée de k-means.

Suffix Tree Clustering (STC) [Zamir 98]

Par rapport aux méthodes précédentes, STC ne cherche pas à ranger chaque document dans un groupe précis. Au contraire, un document peut appartenir à plusieurs groupes (comme Autoclass).

Contrairement aux autres approches, STC ne représente pas un document par la liste non ordonnée des mots qu’il contient. STC s’intéresse aux phrases communes aux documents. La méthode se déroule ainsi :

nettoyage du document comme d’habitude : stoplist, mots fréquents .
lemmatisation rapide (plusieurs, préfixes et suffixes courants : voir l’algorithme de Porter). Remarquez que le lien entre une forme lemmatisée et sa forme d’origine est gardée : quand on montre les mots à l’utilisateur, on peut ainsi utiliser la forme originale et non la forme lemmatisée.
les phrases de chaque document sont identifiées.
création d’un index inversé des phrases : à chaque phrase (et chaque morceau de phrase) on associe la liste des documents dans laquelle elle apparaît.
Pondération de chaque phrase : le score d’une phrase dépend du nombre de mots qu’elle contient ainsi que du nombre de documents dans lesquels elle apparaît. 

Chaque phrase constitue un cluster de base. A chaque phrase est associée la liste des documents dans lesquels elle apparaît. L’étape suivante va consister à fusionner ces clusters de base. Pou décider quand fusionner deux clusters de base, on définit une fonction de similarité entre deux clusters.

 L’algorithme STC a plusieurs propriétés intéressantes :

ses résultats ne dépendent pas de l’ordre de présentation des documents.
il est incrémental (on peut ajouter un nouveau document alors que les autres sont déjà traités et insérés dans l’index inversé des phrases).
il n’est pas nécessaire de donner le nombre de clusters à l’avance; 

Seul bémol : définir manuellement la similarité pour fusionner deux clusters (ici 0.5). Mais les expériences montrent que l’efficacité de STC n’est pas trop sensible à cette valeur.

Bayesian classification : Autoclass

En théorie, cette méthode a de nombreux avantages :

Elle fonctionne avec des valeurs binaires ou réelles.
Elle fournit des classes floues, au sens où elle donne les probabilités qu’un document appartienne à une classe.

Mais elle a aussi des faiblesses :

Elle suppose l’indépendance des attributs, ce qui peut être gênant quand on traite des documents où les attributs sont les mots (ils ne sont pas indépendants !).
Elle fonctionne mal sur des données clairsemées (sparse data) comme c’est le cas des vecteurs de documents ! 

Fonctionnement : soit N documents, décrits chacun par q attributs.

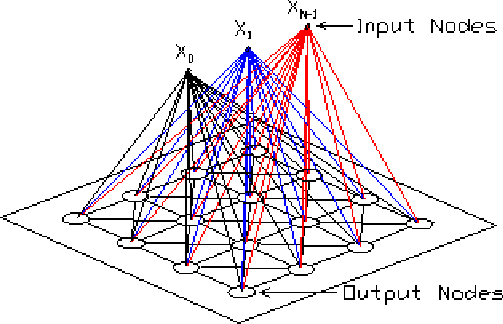
Le but de la méthode est de trouver la classification qui est la plus probable à avoir engendré les N documents.

Self Organizing Maps (SOM) de Kohonen 

figure 1 : une carte SOM

Algorithme pour entraîner la carte :

Choisir les N mots les plus fréquents dans les documents à classer.
Initialiser avec des valeurs aléatoires la matrice map[x][y][z].
x et y : indices des noeuds de la carte (carte 2D)
z : indice des noeuds d'entrée (vecteur)
(chaque noeud de sortie est en effet connecté à tous les noeuds d'entrée).

Présenter (au moins 5 fois) les mêmes vecteurs pour entraîner la carte
Pour chaque vecteur, calculer le noeuds vainqueur (celui qui est le plus proche), avec la formule suivante :

Modifier les connections de ce noeuds et ceux de ses voisins, par exemple avec la formule suivante :

n(t) est une fonction décroissante du temps

Une fois que la carte a été entraînée, il est possible de soumettre un nouveau vecteur (non utilisé pendant l'entraînement) et de calculer le noeud de sortie qui est vainqueur...

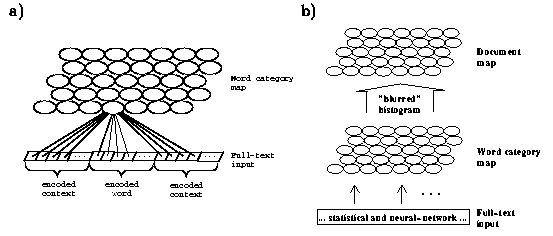
On peut aussi décider d'utiliser ce nouveau vecteur comme un vecteur d'exemple et modifier les poids du réseau. 

Dans http://www.cis.hut.fi/~tho/thesis/index.html#SEC:som, l’auteur suggère deux étapes : a) on constitue une première carte SOM qui groupe les mots en catégories et b) on utilise ce résultat pour sélectionner les mots qui seront utilisés pour représenter les documents. Une fois qu’on a cette représentation (toujours sous forme de vecteur), on peut calculer la SOM des documents.

La décomposition en deux étapes a des avantages :

On réduit considérablement la dimension des vecteurs qui représentent chaque document : la taille du vecteur est au plus égale au nombre de nœuds de la SOM du a) qui correspondent aux catégories des mots.