Les Moteurs de Recherche

on calcule les fréquences de chaque mot dans la collection.

on enlève les mots peu fréquents ou trop fréquents .

on enlève les mots communs (and, but, a, is, are, ...)

on transforme les mots en lemmes (stemming) avec par exemple l’algorithme de Porter qui enlève simplement les suffixes courants (s, es, ing, tion, ed).

on représente chaque document par la liste de ses termes. On peut choisir de mettre un 0 ou un 1 selon que le mot apparaît ou non dans le document. Mais la littérature en recherche d’information suggère de choisir le poids de chaque mot de façon à privilégier les mots qui apparaissent souvent dans certains documents mais peu dans d’autres. Plusieurs formules pour calculer le poids du terme t dans le document i ont été proposées :

Term Frequency (TF) : l’importance d’un terme t est proportionnelle à sa fréquence dans un document
TF(i,t) = fréquence du terme k dans le document i

Inverse Document Frequency : les termes qui apparaissent dans peu de documents sont intéressants
IDF(t) = log(N / df(t))
avec N = nombre de documents
et df(t) = nombre de documents qui contiennent le terme t

IDF est censé améliorer la précision

Mais Salton a montré que les meilleurs résultats étaient obtenus en multipliant TF et IDF :

TDIDF(t,i) = TF(i,t) * IDF(t)

TDIDF = (frequence(m, d) * log(N/n)) / Racine ( Somme sur termes t(tf²(t,d) * log²(N/t)))
N = nombre de documents dans la collection
n = nombre de documents contenant le mot m

Remarque : le modèle vectoriel de Salton propose de représenter chaque document par un vecteur. Soit N le nombre total de termes distincts dans la collection (appelé encore le vocabulaire), on représente chaque document par un vecteur de N éléments. Bien sûr, N est généralement très supérieur au nombre réel des mots présents dans un document. Il en découle que le vecteur contient beaucoup de 0. Pour gagner en place, on représente un document par la liste des termes qu’il contient, avec l’indice du terme. Si le document contient les termes numéro 25, 500 et 768, avec des fréquences respectives de 5,10 et 7, on associera au document la liste de couples (indice,fréquence) suivante : (25,5) (500,10) (768,7).

On doit ensuite choisir une fonction de Distance (ou au contraire de Similarité) qui permet de comparer les documents deux à deux. Voici quelques exemples couramment utilisés et extraites de la littérature en recherche d’information :

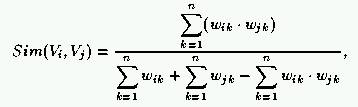
Simple(i,j) = |Intersection(i,j) où Intersection = les mots communs aux documents i et j

Dice(i,j) = |Intersection(i,j)| / (|i| + |j|)

Jaccard(i,j) = |Intersection(i,j)| / |Union(i,j)|

Ce qui revient (avec le modèle vectoriel) :

plus Sim est grand, plus les documents sont similaires

Cosine(x,y) = Somme 0..n(xi * yi) / Racine (Somme 0..n(xi²) * Somme 0..n(yi²))

Remarque : on n’est pas obligé de normaliser avec la division : on peut se contenter de Somme(xi,yi)
avec n = nombre de termes uniques dans la collection
et xi et yi les poids des termes du document i et j

Euclidian(x,y) = Racine( Somme 0..n((xi-yi)²) )

on crée un index inversé : à chaque mot on associe la liste des documents dans lesquels il apparaît. Cet index inversé permet de retrouver rapidement les documents dans lesquels apparaît un mot.

on calcule la matrice de similarité entre tous les documents deux à deux : cette étape est nécessaire pour appliquer la méthode HAC, mais pas pour “ single pass ”.

Remarquons que cette représentation des documents perd l’information sur la position des mots. De plus, elle ne repère pas les co-locations de mots, par exemple “ word wide web ”. Mais il est parfaitement possible de prendre en compte les co-locations : il suffit de générer tous les couples, ou les triplets, etc. des mots qui apparaissent dans les documents. Notons que cette étape augmente le nombre de termes et ajoute du temps de calcul (Maarek utilise une technique “ window sliding ” qui n’ajoute pas trop de temps de calcul). Maarek utilise les couples de mots (qu’il baptise “ lexical affinities ”) pour classer des bookmarks et l’emploi des co-locations tend à améliorer la précision de la classification.

Notons enfin que des recherches récentes ont montré l’intérêt d’utiliser le format des documents HTML pour enrichir la représentation des documents. Typiquement, les mots présents entre des tags <H1> <H2> ... sont a priori plus important et sont donc représentés comme tels (pondération plus grande que les autres mots).

Finalement, selon l’algorithme de clustering utilisé ensuite, le nombre de mots utilisés peut s’avérer très problématique pour les temps de calcul. A titre d’exemple, une simple base d’annotations portant sur 300 documents contient environ 3000 mots distincts (sans compter les mots enlevés par stoplist et les mots inférieurs à 3 lettres), soit une moyenne de 10 mots surlignés par document. Même avec ce faible nombre de termes, une matrice de similarité nécessite en théorie 3000 * 300 entiers, soit 3.5 Moctets de mémoire (entiers codés sur 32 bits, ou encore 4 octets). Les méthodes courantes de sélection de mots se basent sur des critères de fréquence. Les mots les plus fréquents sont gardés et les autres sont éliminés. Attention : cette méthode est bien sûr imparfaite car un mot peut fréquent pourrait bien être important pour représenter une catégorie ! A titre d’exemple, nous citons ici quelques méthodes de réduction du nombre de termes : Latent Semantic Indexing et SOM (voir plus loin).