|
On distingue deux
grandes techniques prédictives du data mining,
la
classification
et
la prédiction
dont le rôle est
d'estimer la valeur d'une variable dite cible en fonction de la
valeur d'un certain nombres d'autres variables dites
indépendantes. Ce qui les distingue est que dans la première la
variable est catégorique et continue dans la deuxième.
La classification ou la
prédiction se déroulent en 4 étapes suivant les techniques
inductives
1- Une étape d'apprentissage, effectuée avec un échantillon
d'individu à classement connu.
2- Une étape de test, pour vérifier le modèle obtenu par
apprentissage en l'appliquant sur un autre échantillon à classement connu.
Sélection le meilleur des modèles obtenus.
3- Une étape de validation, sur un troisième
échantillon à classement connu pour prévoir la qualité des résultats qui seront obtenus lors de
l'application.
4- Une étape d'application, qui s'élargit à l'application sur
l'ensemble de la population.
Qualités
attendues d'une technique de Classification-Prédiction
-
La
précision, la proportion d'individus mal classés doit être
le plus bas.
-
La
concision, les règles du modèles doivent réduites en nombre et
simples.
-
Les
résultats doivent être accessibles et compréhensibles. Quand,
elles sont sous forme de conditions explicites sur les variables
d'origines, elles doivent être facilement programmables pour un
informaticien sous forme de requêtes SQL, par exemple.
-
Insensibilité du modèle aux fluctuations aléatoires et aux valeurs
manquante de certaines variables.
Remarque
Il y a "sur
apprentissage " lors d'une Classification ou une prédiction est
que lorsque il existe une corrélation entre une variable
explicative et une variable cible qui n'existe qu'à l'intérieur de
l'échantillon lui même.
Classification
C'est l'une des
techniques les plus intuitives et des plus répandues dans le data mining, d'une part, parce qu'elle fournit des règles explicites,
ce que ne font les réseaux de neurones. D'autre part, elle possède
un pouvoir prédictif sur des données hétérogènes ou non linéaires
supérieur à celui des autres techniques.
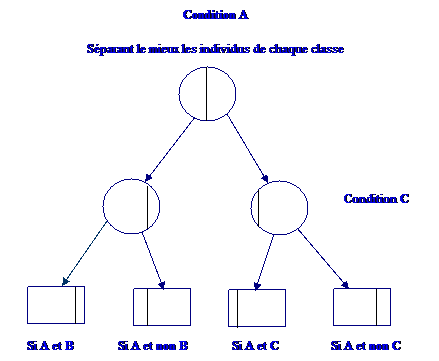
Principe de
l'arbre de décision
Cette technique est
employée en classification pour détecter des critères permettent
de répartir les individus d'une population en n classes (n = 2).
On commence par choisir
la variable qui par ses modalités sépare le mieux les individus de
chaque classe de façon à avoir des sous population appelées
noeuds contenant chacune le plus possible d'individus d'une
même classe. O réitère ensuite l'opération sur chaque nouveau
noeud obtenu jusqu'à ce que la séparation des individus ne soit
plus possible ou souhaitable.
Par construction, les
noeuds terminaux ou feuilles sont majoritairement
constitués d'individus d'une même classe.
Ainsi, un individu est
affecté à une feuille et donc à une certaine classe avec une
certaine probabilité s'il satisfait l'ensemble des règles
permettant d'arriver à cette feuille.
L'ensemble des règles de
toutes les feuilles constituent le modèle de classification.
Construction de
l'arbre
La première étape
consiste en un choix judicieux de la variable qui va séparer les
individus de chaque classe: le critère (C1) de choix de la
variable et de sa valeur testée dépend de chaque type d'arbre.
Si l'échantillon est
constitué de n individus et si les variables explicatives sont
toutes numériques, il y a n.m candidats possibles pour la
condition de séparation qui pourrait être Var1<a1, Var1<b1,....,
Var1<a2, etc.

Une fois la meilleure
séparation trouvée, on l'applique, on réitère l'opération sur
chaque noeud pour augmenter la discrimination ce qui donne
naissance à chaque noeud à un ou plusieurs noeuds fils. Chaque
noeud fils donne à son tour naissance à d'autres noeuds et
ainsi de suite jusqu'à ce que le processus ne peut plus être
répété ou un critère (C2) d'arrêt d'approfondissement de l'arbre
est satisfait.
Si chaque noeud possède
2 fils l'arbre est binaire. Le chemin entre la racine et la
feuille est l'expression de la règle pour une classe.
Exemple
Les clients dont l'âge <
x, les revenus < y et le nombre de comptes >= z appartiennent dans
n% des cas à la classe C. Le pourcentage n est un score
d'appartenance à la classe C. La densité d'un noeud st le rapport
de son effectif à celui de la population totale.
Le critère d'arrêt
dépend comme celui de la séparation (C1), du type et du
paramétrage de l'arbre, il combine souvent plusieurs
règles.
Qualité de l'arbre
suffisante
Profondeur maximale de
l'arbre atteinte
Effectif de chaque noeud
est inférieur à une valeur fixée.
Nombre maximal de
feuilles atteint.
Critère de séparation
(C1)
Les trois principaux
critères sont
Le critère de chi-2,
prévu pour les variables explicatives de type catégorique.
Le critère de Gini, pour
tout type de variables explicatives.
L'entropie, ou
l'information, pour tous les types de variables explicatives.
Un des critères les plus
utilisés est celui de Gini défini par

où les fi, i de 1
à n sont les fréquences relatives dans le noeud des n classes
considérées. Plus, le noeud est pure plus son indice de Gini est
bas. Cet indice mesure la probabilité que deux individus choisi
aléatoirement dans un noeud appartiennent à 2 classes différentes.
Chaque séparation entre
deux noeuds fils doit provoquer la plus grande hausse de pureté
donc la plus grande baisse de l'indice de Gini. Ainsi, il faut
maximiser:
indice de
Gini(avant séparation) - [indice de Gini(fils gauche) + indice de
Gini(fils droit)]
L'entropie est calculée
comme suit:
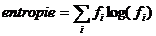
De même, pus les classes
sont uniformément distribuées à l'intérieur d'un noeud, plus
l'entropie est élevée. Plus le noeud est pure, plus l'entropie est
basse. Il faut donc, maximiser:
entropie(avant séparation) - [entropie(fils gauche) +
entropie(fils droit)]
La complexité de
l'élaboration d'un modèle par arbre de décision vient de ce que,
si une variable explicative catégorique X a un ensemble E de n
valeurs possibles x1,...,xn de X, toute condition de séparation
sur cette variable sera de la forme:
 X
appartient à E' où E' inclus dans E - X
appartient à E' où E' inclus dans E -
et on voit qu'il y
a
 conditions de séparation
possibles sur cette variable .
conditions de séparation
possibles sur cette variable .
Pour une variable
explicative continue X, la complexité est liée au ri des valeurs
x1....xn, puisque une fois dans l'ordre il suffit de trouver
l'indice k tel que la condition X<= moyenne(xk,xk+1) soit
la meilleure possible.
Il y a donc n-1
conditions de séparation possibles sur cette variable.
Répartition des
individus dans les noeuds
Une fois l'arbre construit et les critères de division de chaque
noeud obtenus, chaque individu peut être affecté à exactement une
feuille. Chaque feuille contient une proportion d'individus de
chaque classe C. On note pc la proportion d'individus appartenant
à la classe C. Alors, la classe C pour laquelle pc est maximale
est considérée comme la classe de cette feuille. Les individus de
cette feuille sont considérés comme classés dans C avec une
probabilité pc et un taux d'erreur 1-pc.
L'élagage
Il faut raccourcir la
longueur des branches d'arbres afin d'éliminer les très petits
noeuds sans signification statistique réelle: il faut au moins 20
à 30 individus par noeud. L'élagage permet d'éviter un sur
apprentissage.
Inconvénients des arbres de décision
L'arbre détecte les
minima locaux et non globaux. Il n'utilise pas simultanément
toutes les variables explicatives, mais séquentiellement.
Le choix d'une division
pour un noeud à certain niveau de l'arbre n'est plus jamais
remis en cause.
En conséquence, la
modification d'une seule variable, si elle est proche de la racine
peut entièrement modifier l'arbre.
La
prédiction par arbre de décision
Les arbres de décision
relatifs à la classification peuvent être utilisés pour la
prédiction. Il suffit de modifier le critère de séparation (C1)
Il faut choisir
des fils qui minimisent la variance intra classe et qui maximisent
la variance interclasse
 |