Introduction
Le but de ce TD est de vous initier à la création et à l'utilisation de quadtrees pour faire du frustum culling.
Un petit conseil, lisez chaque question attentivement et en entier...
Un quadtree est une structure arborescente dans laquelle chaque noeud est associé à une partie d'une surface plane et rectangulaire. Chaque noeud peut avoir 4 fils représentant quatre subdivisions rectangulaires régulières de la surface de leur père (Voir l'image 1 ci-dessous pour un exemple de subdivision et l'arbre associé à cette subdivision).
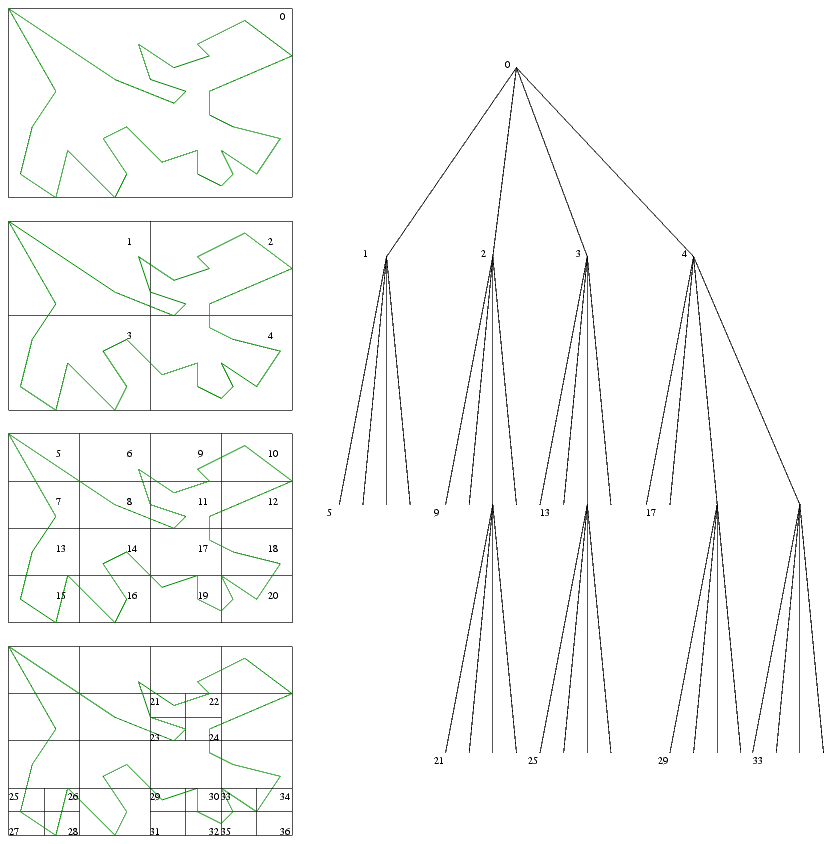
|
On se sert généralement d'une telle structure pour répartir les différents éléments d'une scène 2D dans différents noeuds. On peut alors par exemple déterminer les éléments visibles dans un certain sous-espace en parcourant l'arbre et en rejetant les noeuds que n'intersectent pas le sous-espace (Dans l'image 2 ci-dessous, seuls les segments situés dans les noeuds bordés de rouge seront potentiellement visibles).
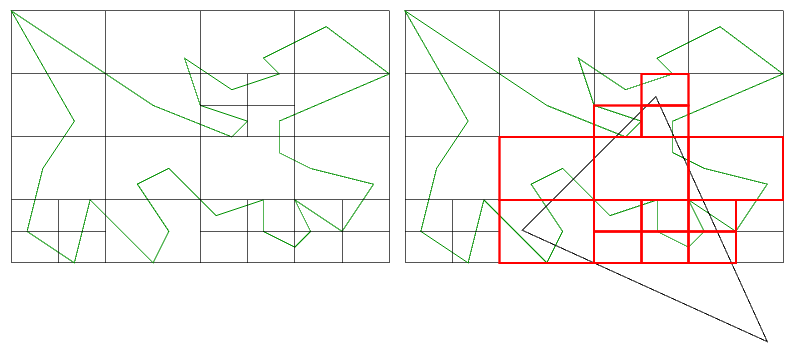
|
Exercice 1
Proposez et implémentez un algorithme permettant de construire récursivement un tel arbre à partir d'un ensemble de segments. Cet algorithme aura deux paramètres importants:
- le nombre maximal de segments qu'on accepte de stocker dans un noeud, 0 indiquant qu'on ne souhaite pas imposer de maximum;
- la profondeur maximale que peut atteindre l'arbre, une valeur négative de ce paramètre indiquant qu'on ne souhaite pas de limite de profondeur.
Votre programme devra prendre en ligne de commande ces deux paramètres ainsi que le nom d'un fichier contenant l'ensemble des segments et que le nom d'un fichier de sortie qui contiendra le résultat de votre algorithme.
Le fichier d'entrée (On vous propose un exemple de fichier d'entrée) sera composé de lignes. Chaque ligne contiendra deux couples de coordonnées (x, y) décrivant les extrémités du segment. On considérera qu'à la première ligne correspondra le segment d'identifiant 0 et que les lignes suivantes verront cet identifiant s'incrémenter de 1 par ligne.
Le fichier de sortie contiendra une première ligne contenant les valeurs xmin, xmax, ymin, ymax décrivant la zone contenant la scène. Ensuite on écrira un noeud par ligne. Chaque noeud commencera par une lettre décrivant le type du noeud. Ce type pourra être I (comme noeud interne) ou F (comme noeud feuille). Cette lettre sera suivie des indices des segments contenus au moins partiellement dans ce noeud. Les lignes sont écrites en parcourant l'arbre en profondeur d'abord.
Exercice 2
On suppose maintenant que les segments de la question 1. représentent une vue de dessus des murs d'un niveau d'un quelconque FPS (oui, oui, un FPS 2.5D). Proposez dans un premier temps une solution permettant de réaliser l'affichage de ces murs ainsi qu'une méthode de déplacement dans la scène ainsi créée. On supposera que l'unité de mesure est le mètre, que les murs ont une hauteur de 2.5m et que la hauteur des yeux par rapport au sol est de 1.8m.
Une fois cette première étape réalisée, vous proposerez une solution utilisant le quadtree créé à l'étape précédente permettant de n'afficher que les pans de mur au moins partiellement visibles.
Exercice 3
Un octree étant une version tridimensionnelle d'un quadtree (c'est à dire qu'un noeud cubique de base est subdivisé en 8 noeuds fils), proposez une solution permettant de partitionner puis d'afficher un volume rempli de sphères ne s'intersectant pas.
Les réponses à ces 3 questions sont à renvoyer par email (1 message par groupe de TP) à votre chargé de TD pour dans 2 semaines au plus tard c'est à dire avant 12h, le mardi 25 octobre 2005.
Bon courage