






Le but du projet est de faire un programme qui prend une séquence de valeurs comme modèle, et produit un générateur aléatoire de séquences qui ressemblent au modèle.
Soit O un ensemble d'objets du même type.
Le modèle est une séquence d'objets S=[o1,o2,...,on], avec n
grand. Si P=[p1,...,pm] est une séquence de m ≤ n objets, on note
n(P,S) le nombre de fois qu'apparaît P dans S. Par exemple,
n([a,a,b,a], [c,a,a,b,a,a,b,a,b,b]) = 2.
La chaîne de Markov CM d'ordre k ≥ 2 de S donne,
pour chaque séquence P=[p1,...,p{k-1}], une loi de probabilité sur
l'ensemble des objets O. Ainsi, CM(P,o) est la probabilité que l'objet
o apparaisse à la suite de la séquence P.
Celle-ci est donc obtenue à partir du modèle S par
| CM(P,o)= | n([p1,...,p{k-1},o],S) |
| n(P,S) |
Le projet consiste à calculer à partir d'une séquence d'objets une représentation de la fonction CM, puis de s'en servir pour générer aléatoirement des séquences d'objets.
Dans un premier temps, réalisez une classe ProbaSet<O> qui représente une ensemble d'objets pondéré dans N (chaque objet o de l'ensemble a un poids entier p(o)). La classe possède obligatoirement les méthodes suivantes :
Réalisez une classe KBuffer<O> qui permet de parcourir les blocs de k objets d'une séquence d'objets de type O. Elle doit posséder les méthodes suivantes :
Réalisez une classe MarkovChain<O> qui simule l'application CM de la partie I. En fait, on associe à chaque séquence P=[p1,...,p{k-1}] un objet de la classe ProbaSet<O> contenant, pour chaque objet o qui peut suivre P dans S, l'objet o avec le poids n([p1,...,p{k-1},o],S). Par exemple si S est une séquence de caractères S="aabaabbaaba" et que k=4, l'objet MarkovChain<Character> associe à la séquence "aab" le ProbaSet<Character> {(a,2),(b,1)} puisque a suit deux fois "aab" dans S et b une fois.
Elle doit posséder les méthodes suivantes :
Réalisez une classe MarkovChainBuilder qui contient des méthodes static pour générer des chaînes de markov :
Le rendu du projet consiste en une archive zip contenant les sources du projet et des fichiers permettant de tester le projet, ainsi qu'un rapport en pdf. L'archive doit être nommée JavaTTT_XXXX_YYYY.zip où XXXX et YYYY sont les noms des auteurs du projet; le désarchivage doit créer un répertoire de même nom JavaTTT_XXXX_YYYY dans lequel se trouvent tous les fichiers rendus.
Dans votre rapport :
On considère pour cet exemple une séquence S contenant n=10 objets représentés par des images :


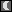







On prend k=3. Il s'agit donc dans un premier temps, de
fabriquer une simulation c de la CM en associant à tout
couple (k-1=2) d'images (o1,o2) une liste probabilisée d'images. Elle
est calculée, pour chaque couple (o1,o2) qui a une image, en regardant
quels sont les images qui suivent (o1,o2) dans S. Par exemple, la
séquence 
 apparaît 3 fois dans
S; une fois suivie par
apparaît 3 fois dans
S; une fois suivie par 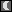 et deux fois suivie par
et deux fois suivie par
 . En procédant ainsi pour tous les couples
possibles, on a au final :
. En procédant ainsi pour tous les couples
possibles, on a au final :
c(
 ) = { (
) = { (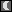 ,1), (
,1), ( ,2) }
,2) }
c(
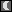 ) = { (
) = { ( ,1) }
,1) }
c(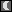
 ) = { (
) = { ( ,1) }
,1) }
c(
 ) = { (
) = { ( ,1), (
,1), ( ,2) }
,2) }
c(
 )= { (FIN,1)
}
)= { (FIN,1)
}
Une fois la CM calculée, on peut générer aléatoirement des
séquences. Pour cela on se donne un paramètre size, ici size=6,
qui correspond au nombre maximum d'objets générés, et d'un début start qui
est une séquence de taille k-1. Ici il s'agit donc d'un couple, et on
prend start=
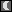 pour l'exemple.
pour l'exemple.
La génération se déroule de la façon suivante, au début P=start et évolue au fur et à mesure. Le résultat est une séquence R qui est vide au début :

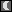 : on tire au sort dans
c(P)= { (
: on tire au sort dans
c(P)= { ( ,1) }. Comme il n'y a qu'un
élément, le tirage au sort retourne
,1) }. Comme il n'y a qu'un
élément, le tirage au sort retourne  . On enlève le
premier élément de P, et on ajoute l'élément tiré au sort à la
fin. L'élément retiré est ajouté au résultat : R =
. On enlève le
premier élément de P, et on ajoute l'élément tiré au sort à la
fin. L'élément retiré est ajouté au résultat : R =  .
.
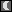
 : on tire au sort dans
c(P)= { (
: on tire au sort dans
c(P)= { ( ,1) }. Comme il n'y a qu'un
élément, le tirage au sort retourne
,1) }. Comme il n'y a qu'un
élément, le tirage au sort retourne  . On enlève le
premier élément de P, et on ajoute l'élément tiré au sort à la
fin. L'élément retiré est ajouté au résultat : R =
. On enlève le
premier élément de P, et on ajoute l'élément tiré au sort à la
fin. L'élément retiré est ajouté au résultat : R = 
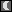 .
.

 : on tire au sort dans
c(P)= { (
: on tire au sort dans
c(P)= { ( ,1), (
,1), ( ,2)
}. On a 1 chance sur 3 de tirer au sort
,2)
}. On a 1 chance sur 3 de tirer au sort  et 2 chances sur 3 de tirer au sort
et 2 chances sur 3 de tirer au sort  . On suppose
que le hasard choisit
. On suppose
que le hasard choisit  . On enlève le
premier élément de P, et on ajoute l'élément tiré au sort à la
fin. L'élément retiré est ajouté au résultat : R =
. On enlève le
premier élément de P, et on ajoute l'élément tiré au sort à la
fin. L'élément retiré est ajouté au résultat : R = 
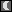
 .
.

 : on tire au sort dans
c(P)= { (
: on tire au sort dans
c(P)= { (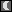 ,1), (
,1), ( ,2)
}. On a 1 chance sur 3 de tirer au sort
,2)
}. On a 1 chance sur 3 de tirer au sort 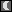 et 2 chances sur 3 de tirer au sort
et 2 chances sur 3 de tirer au sort  . On suppose
que le hasard choisit
. On suppose
que le hasard choisit 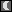 . On enlève le
premier élément de P, et on ajoute l'élément tiré au sort à la
fin. L'élément retiré est ajouté au résultat : R =
. On enlève le
premier élément de P, et on ajoute l'élément tiré au sort à la
fin. L'élément retiré est ajouté au résultat : R = 

 .
.

 : on s'arrête, car la
somme des tailles de R et de P vaut 6, on a généré suffisament
d'images. On ajoute P à la fin de R, le résultat de cette génération
aléatoire est donc
: on s'arrête, car la
somme des tailles de R et de P vaut 6, on a généré suffisament
d'images. On ajoute P à la fin de R, le résultat de cette génération
aléatoire est donc