Programmation C++

Master M2 Informatique --- Feuille n° 3

Résumé:

On se propose dans ce TD de manipuler des masques de bits calculés à la compilation. Les entiers (non signés) seront assimilés à des tableaux de bits dont la première case est le bit de poids faible.

On peut en C++ définir une classe paramétrée par des entiers et spécialiser cette classe pour certaines valeurs:

template<unsigned N>
struct Fibonacci{
  static const unsigned res= Fibonacci<N-1>::res + Fibonacci<N-2>::res;
};

template<>
struct Fibonacci<1>{
  static const unsigned res=1;
};


template<>
struct Fibonacci<0>{
  static const unsigned res=0;
};

Noter que si la classe a plusieurs paramètres, on peut ne spécialiser que selon l'un d'entre eux. Pour des valeurs données, c'est toujours la classe qui a le moins de paramètres libres qui sera choisie.

Exercice n° 1

Écrire une classe template IntervalMask telle que IntervalMask<Begin,Size>::val est l'entier dont Size bits à partir du bit Begin valent 1. Par exemple, la valeur décimale de IntervalMask<3,4>::val est 120.

Exercice n° 2

Écrire une classe template BinInfo paramétrée par un entier N et qui contient trois constantes:

weakBit : un booléen qui indique la valeur du bit de poids faible;
bloc0 : qui donne le nombre i maximal tel que tous les bits de [0;i[ sont à 0;
bloc1 : qui donne le nombre j maximal tel que tous les bits de [i;i+j[ sont à 1>. Pour N=0, bloc0 vaut le nombre de bits dans un int et bloc1 est nul.

Exercice n° 3

On désire calculer tous les masques sur les N premiers bits dont exactement K bits valent 1. L'algorithme suivant permet d'énumérer les masques qui ont cette propriété.

Le premier est IntervalMask<0,K>::val;
Le dernier est IntervalMask<N-K,K>::val;
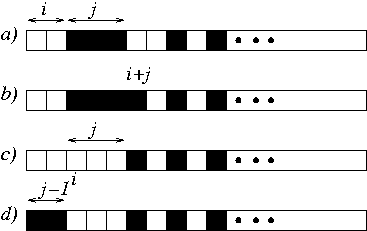
À partir d'un masque de cette famille, on obtient le masque suivant comme suit:
a) on calcule le nombre i de bits à 0 au début du masque et la longueur j du premier bloc de 1;
b) on met le bit i+j à 1;
c) on met les bits de [i;i+j[ à 0;
d) on met les bits de [0;j-1[ à 1.

Écrire une classe Next paramétrée par un masque M et qui calcule le masque qui suit M.

Exercice n° 4

Justifier que le nombre de masques sur les N premiers bits dont exactement K bits valent 1 est égal à binomial(n,k). On rappelle que binomial(n,k) est calculable récursivement;

binomial(n,k)=0 si k>n,
binomial(n,k)=1 si k=0 ou k=n,
binomial(n,k)=binomial(n-1,k)+binomial(n-1,k-1) sinon.

Écrire la classe Binomial de sorte que Binomial<N,K>::val est une constante égale à binomial(n,k).

Exercice n° 5

Écrire la classe ArrayMask de sorte que ArrayMasque<N,K,I>::val soit le I-ème masque ayant K bits à 1 parmi les N premiers. Si I est trop grand, cette valeur devra être nulle.

Exercice n° 6

Écrire une fonction template print telle que print<M,N>() affiche les N premiers bits de M. Écrire une classe template For de sorte que For<I,J,K,N>::print() affiche tous les masques ayant K bits à 1 parmi les N premiers du I-ème masque jusqu'au J-ème.