- preprocessing phase in O(m) time and space complexity;
- searching phase in O(n) time complexity;
- performs
 n text character comparisons in the worst case.
n text character comparisons in the worst case.




 n text character comparisons in the worst case.
n text character comparisons in the worst case.The Apostolico-Crochemore uses the kmpNext shift table (see chapter Knuth, Morris and Pratt algorithm) to compute the shifts.
Let  =0 if x is a power of a single character (x=cm with c in
=0 if x is a power of a single character (x=cm with c in  ) and
) and  be equal to the position of the first character of x different from x[0] otherwise (x=a
be equal to the position of the first character of x different from x[0] otherwise (x=a bu for a, b in
bu for a, b in  , u in
, u in  * and a
* and a  b). During each attempt the comparisons are made with pattern
positions in the following order:
b). During each attempt the comparisons are made with pattern
positions in the following order:  ,
,  +1, ... , m-2, m-1, 0, 1, ... ,
+1, ... , m-2, m-1, 0, 1, ... ,  -1.
-1.
 |
the window is positioned on the text factor y[j .. j+m-1]; |
 |
0  k k   and x[0 .. k-1]=y[j .. j+k-1]; and x[0 .. k-1]=y[j .. j+k-1]; |
 |
  i < m and x[ i < m and x[ .. i-1]=y[j+ .. i-1]=y[j+ .. i+j-1]. .. i+j-1]. |
The initial triple is ( ,0,0).
,0,0).
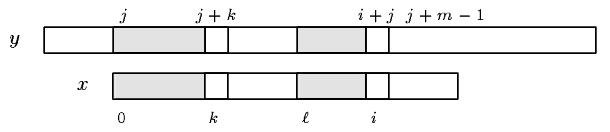
Figure 11.1: At each attempt of the Apostolico-Crochemore algorithm we consider a triple (i,j,k).
We now explain how to compute the next triple after (i,j,k) has been computed.
 |
i =  If x[i] = y[i+j] then the next triple is (i+1, j, k). If x[i]  y[i+j] then the next triple is ( y[i+j] then the next triple is ( , j+1, max{0, k-1}). , j+1, max{0, k-1}). |
 |
 < i < m < i < mIf x[i] = y[i+j] then the next triple is (i+1, j, k). If x[i]  y[i+j] then two cases arise depending on the value of kmpNext[i]: y[i+j] then two cases arise depending on the value of kmpNext[i]:
|
 |
i =m If k <  and x[k]=y[j+k] then the next triple is (i, j, k+1). and x[k]=y[j+k] then the next triple is (i, j, k+1).Otherwise either k <  and x[k] and x[k]  y[j+k], or k= y[j+k], or k= . If k= . If k= an occurrence of x is reported. In both cases the next triple is computed in the same manner as in the case where an occurrence of x is reported. In both cases the next triple is computed in the same manner as in the case where  < i < m. < i < m. |
The preprocessing phase consists in computing the table kmpNext and the integer  . It can be done in O(m) space and time. The searching phase is in O(n) time complexity and furthermore the Apostolico-Crochemore algorithm performs at most
. It can be done in O(m) space and time. The searching phase is in O(n) time complexity and furthermore the Apostolico-Crochemore algorithm performs at most  n text character comparisons in the worst case.
n text character comparisons in the worst case.
The function preKmp is given chapter Knuth, Morris and Pratt algorithm.
void AXAMAC(char *x, int m, char *y, int n) {
int i, j, k, ell, kmpNext[XSIZE];
/* Preprocessing */
preKmp(x, m, kmpNext);
for (ell = 1; x[ell - 1] == x[ell]; ell++);
if (ell == m)
ell = 0;
/* Searching */
i = ell;
j = k = 0;
while (j <= n - m) {
while (i < m && x[i] == y[i + j])
++i;
if (i >= m) {
while (k < ell && x[k] == y[j + k])
++k;
if (k >= ell)
OUTPUT(j);
}
j += (i - kmpNext[i]);
if (i == ell)
k = MAX(0, k - 1);
else
if (kmpNext[i] <= ell) {
k = MAX(0, kmpNext[i]);
i = ell;
}
else {
k = ell;
i = kmpNext[i];
}
}
}
Preprocessing phase
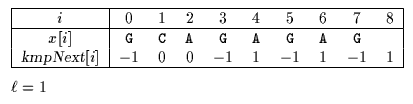
kmpNext table used by Apostolico-Crochemore algorithm
Searching phase



