The design of the Colussi algorithm follows a tight analysis of the Knuth, Morris and Pratt algorithm.
- The set of pattern positions is divided into two disjoint subsets. Then each attempt consists in two phases:
-
 |
in the first phase the comparisons are performed from left to right with text characters aligned with pattern position for which the value of the kmpNext function is strictly greater than -1. These positions are called noholes; |
-
 |
the second phase consists in comparing the remaining positions (called holes) from right to left. |
- This strategy presents two advantages:
-
 |
when a mismatch occurs during the first phase, after the appropriate shift it is not necessary to compare the text characters aligned with noholes compared during the previous attempt; |
-
 |
when a mismatch occurs during the second phase it means that a suffix of the pattern matches a factor of the text, after the corresponding shift a prefix of the pattern will still match a factor of the text, then it is not necessary to compare this factor again. |
Definitions
Then assume that x is aligned with y[j .. j+m-1]. If x[h[k]]=y[j+h[k]] for 0  k < r < nd and x[h[r]]
k < r < nd and x[h[r]]  y[j+h[r]]. Let j’ = j+kmin[h[r]].
y[j+h[r]]. Let j’ = j+kmin[h[r]].
Then there is no occurrence of x beginning in y[j .. j’] and x can be shifted by kmin[h[r]] positions to the right.
Moreover x[h[k]]=y[j’+h[k]] for 0  k < first[h[r]-kmin[h[r]]] meaning that the comparisons can be resume with x[h[first[h[r]-kmin[h[r]]]]] and y[j’+h[first[h[r]-kmin[h[r]]]]].
k < first[h[r]-kmin[h[r]]] meaning that the comparisons can be resume with x[h[first[h[r]-kmin[h[r]]]]] and y[j’+h[first[h[r]-kmin[h[r]]]]].
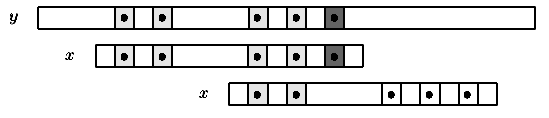
Figure 9.1: Mismatch with a nohole. Noholes are black circles and are compared from left to right.
In this situation, after the shift, it is not necessary to compare the first two noholes again.
If x[h[k]]=y[j+h[k]] for 0  k < r and x[h[r]]
k < r and x[h[r]]  y[j+h[r]] with nd
y[j+h[r]] with nd  r < m. Let j’=j+rmin[h[r]]. Then there is no occurrence of x beginning in y[j .. j’] and x can be shifted by kmin[h[r]] positions to the right.
r < m. Let j’=j+rmin[h[r]]. Then there is no occurrence of x beginning in y[j .. j’] and x can be shifted by kmin[h[r]] positions to the right.
Moreover x[0 .. m-1-rmin[h[r]]]=y[j’ .. j+m-1] meaning that the comparisons can be resume with x[h[first[m-1-rmin[h[r]]]]] and y[j’+h[first[m-1-rmin[h[r]]]]].

Figure 9.2: Mismatch with a hole. Noholes are black circles and are compared from left to right
while holes are white circles and are compared from right to left.
In this situation, after the shift, it is not necessary to compare the matched prefix of the pattern again.
To compute the values of kmin, a table hmax is used and defined as follows: hmax[k] is such that x[k .. hmax[k]-1]=x[0 .. hmax[k]-k-1] and x[hmax[k]]  x[hmax[k]-k].
x[hmax[k]-k].
The value of nhd0[i] is the number of noholes strictly smaller than i.
- We can now define two functions shift and next as follows:
-
 |
shift[i]=kmin[h[i]] and next[i]=nhd0[h[i]-kmin[h[i]]] for i < nd; |
-
 |
shift[i]=rmin[h[i]] and next[i]=nhd0[m-rmin[h[i]]] for nd  i < m; i < m; |
-
 |
shift[m]=rmin[0] and next[m]=nhd0[m-rmin[h[m-1]]]. |
Thus, during an attempt where the window is positioned on the text factor y[j .. j+m-1], when a mismatch occurs between x[h[r]] and y[j+h[r]] the window must be shifted by shift[r] and the comparisons can be resume with pattern position h[next[r]].
The preprocessing phase can be done in O(m) space and time. The searching phase can then be done in O(n) time complexity and furthermore at most  n text character comparisons are performed during the searching phase.
n text character comparisons are performed during the searching phase.
int preColussi(char *x, int m, int h[], int next[],
int shift[]) {
int i, k, nd, q, r, s;
int hmax[XSIZE], kmin[XSIZE], nhd0[XSIZE], rmin[XSIZE];
/* Computation of hmax */
i = k = 1;
do {
while (x[i] == x[i - k])
i++;
hmax[k] = i;
q = k + 1;
while (hmax[q - k] + k < i) {
hmax[q] = hmax[q - k] + k;
q++;
}
k = q;
if (k == i + 1)
i = k;
} while (k <= m);
/* Computation of kmin */
memset(kmin, 0, m*sizeof(int));
for (i = m; i >= 1; --i)
if (hmax[i] < m)
kmin[hmax[i]] = i;
/* Computation of rmin */
for (i = m - 1; i >= 0; --i) {
if (hmax[i + 1] == m)
r = i + 1;
if (kmin[i] == 0)
rmin[i] = r;
else
rmin[i] = 0;
}
/* Computation of h */
s = -1;
r = m;
for (i = 0; i < m; ++i)
if (kmin[i] == 0)
h[--r] = i;
else
h[++s] = i;
nd = s;
/* Computation of shift */
for (i = 0; i <= nd; ++i)
shift[i] = kmin[h[i]];
for (i = nd + 1; i < m; ++i)
shift[i] = rmin[h[i]];
shift[m] = rmin[0];
/* Computation of nhd0 */
s = 0;
for (i = 0; i < m; ++i) {
nhd0[i] = s;
if (kmin[i] > 0)
++s;
}
/* Computation of next */
for (i = 0; i <= nd; ++i)
next[i] = nhd0[h[i] - kmin[h[i]]];
for (i = nd + 1; i < m; ++i)
next[i] = nhd0[m - rmin[h[i]]];
next[m] = nhd0[m - rmin[h[m - 1]]];
return(nd);
}
void COLUSSI(char *x, int m, char *y, int n) {
int i, j, last, nd,
h[XSIZE], next[XSIZE], shift[XSIZE];
/* Processing */
nd = preColussi(x, m, h, next, shift);
/* Searching */
i = j = 0;
last = -1;
while (j <= n - m) {
while (i < m && last < j + h[i] &&
x[h[i]] == y[j + h[i]])
i++;
if (i >= m || last >= j + h[i]) {
OUTPUT(j);
i = m;
}
if (i > nd)
last = j + m - 1;
j += shift[i];
i = next[i];
}
}
 n text character comparisons in the worst case.
n text character comparisons in the worst case.




 i
i  x[i]
x[i]

