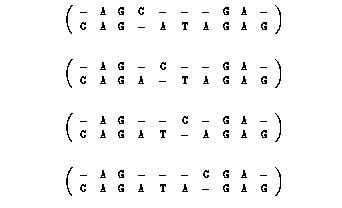If we set
Sub(a,a) = 0 for
![]() and
Sub(a,b) = Del(a) +
Ins(b) for
and
Sub(a,b) = Del(a) +
Ins(b) for
![]() and
and
![]() .
Then T[m-1,n-1] represents the
edit distance between x and y where a deletion of
a followed by an insertion of b is
always prefered to a substitution of a by b.
The solution to the dual problem gives the length of a longest
common subsequence of x and y.
.
Then T[m-1,n-1] represents the
edit distance between x and y where a deletion of
a followed by an insertion of b is
always prefered to a substitution of a by b.
The solution to the dual problem gives the length of a longest
common subsequence of x and y.
The notion of longest common subsequence of two strings is used to compare file. The diff command of the UNIX system is based on this notion where the lines of the files are considered as the symbols of the alphabet.
A subsequence of a word x is obtained by deleting zero, one or
several letters of x.
More formally
w0w1···wi-1
is a subsequence of
x0x1···xm-1
if there exists a strictly increasing sequence of integers
(k0, k1, ...,
ki-1)
such that for 0 <= k <= i-1,
![]() .
.
A word w is a longest common subsequence of x and y if w is a subsequence of x, a subsequence of y and its length is maximal.
Let us remark that two words x and y can have several different longest common subsequences. The set of the longest common subsequences of x and y is denoted by Lcs(x,y).
The (unique) length of the elements of Lcs(x,y) is denoted by lcs(x,y).
A straightforward method to compute lcs(x,y) consists in considering all the subsequences of x, checking if they are subsequences of y and keeping the longest. The word x of length m has 2m subsequences, thus this method is not applicable for high values of m.
Let x a word of length m and y a word of length n. Using dynamic programming yields to compute lcs(x,y) in O(mn) time and space complexity. The method computes length of longest common subsequences of longer and longer prefixes of the two words x and y.
For that we used a two-dimensional table T of size (m+1) * (n+1) defined as follows:
T[i,-1] = T[-1,j] = 0 for -1 <= i <= m-1 and -1 <= j <= n-1
and for 0 <= i <= m-1 and 0 <= j <= n-1
T[i,j] = lcs( x0x1···xi, y0y1···yj)
The computation of
lcs(x,y) = T[m-1,n-1]
if based on a simple
observation which leads to the following recurrence formula:
for 0 <= i <= m-1 and 0 <= j <= n-1
![]()
PROPOSITION For 0 <= i <= m-1 and 0 <= j <= n-1:
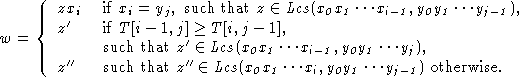
PROOF
Let
![]() ,
,
![]() and
and
![]() .
.
z is a longest common subsequence of
x0x1···xi-1
and
y0y1···yj-1.
z' is a longest common subsequence of
x0x1···xi-1
and
y0y1···yj.
z'' is a longest common subsequence of
x0x1···xi
and
y0y1···yj-1.
|z| = T[i-1,j-1],
|z'| = T[i-1,j] and
|z''| = T[i,j-1].
Then clearly if
xi = yj,
T[i,j]=1+T[i-1,j-1] and
w = zxi is a longest common subsequence of
x0x1···xi
and
y0y1···yj.
If
![]() then let us consider the following two cases:
then let us consider the following two cases:
This formula is used by the algorithm LONGEST-COMMON-SUBSEQUENCE to compute all the values of T.

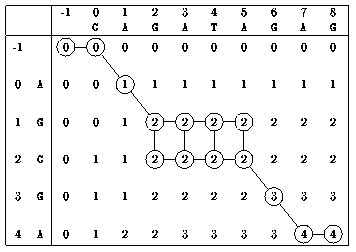
This computation is evidently in O(mn) time and space complexity. It is the possible to exhibit a longest common subsequence of x and y tracing back in the table from T[m-1,n-1] to T[-1,-1].

Example:
AGGA is a longest common subsequence of x = AGCGA and y = CAGATAGAG.
This corresponds to the four following alignments: