Résumé du cours 3

Introduction à la cryptanalyse linéaire

Cette technique s'applique aux réseaux de permutations-substitutions (SPN). C'est une attaque à texte clair connu. L'attaquant doit disposer d'un grand nombre de couples (X,Y) de textes clairs/textes chiffrés.

L'idée est de trouver une relation linéaire

entre certains bits de l'entrée X, de la sortie Y et de la clé K qui ne soit pas aléatoire. Si les bits d'entrée et de sortie étaient des variables aléatoires indépendantes, un telle relation serait vérifiée en moyenne une fois sur deux (probabilité ½).

Supposons qu'on en connaisse une qui ait une probabilité p aussi différente de ½ que possible.

Algorithme 1 de Matsui.

1. Collecter un grand nombre N de couples (X,Y)

2. Pour chaque couple, calculer le membre gauche de l'expression linéaire. Soit T le nombre de résultats nuls.

3. Si T est plus grand que N/2 et si p > ½ , on conclut que le membre droit doit être 0

4. Si < N/2 et si p < ½ , on conclut encore que le membre droit est 0

5. Dans les autres cas, on conclut que le membre droit est 1

Ce n'est pas très efficace, mais on peut faire mieux avec le même principe. On va cette fois tester toutes les valeurs possibles des bits de la clé concernés par le membre droit de la relation.

Algorithme 2 de Matsui.

1. Collecter un grand nombre N de couples (X,Y)

2. Pour chaque jeu de bits de clé candidats, on calcule une valeur T égale au nombre de fois que la relation est vérifiée

3. On sélectionne les candidats qui ont un T le plus éloigné possible de N/2.

Pour mettre en oeuvre cette technique, il faut commencer par calculer des « approximations linéaires » des seuls éléments non linéaires du système, à savoir les S-boîtes.

Si X et Y sont l'entrée et la sortie de la S-boîte considérée, sa table d'approximation linéaire est une matrice dont l'entrée (i,j) est , où T(i,j) est le nombre de fois que la relation linéaire X|i = Y|j codée par les bits 1 de i et j est vérifiée.

On trouvera ici un programme pour calculer la table d'approximation linéaire de la S-boîte de easy1.

A partir de deux expressions ayant un biais élevé, on peut construire une attaque avec le schéma suivant.

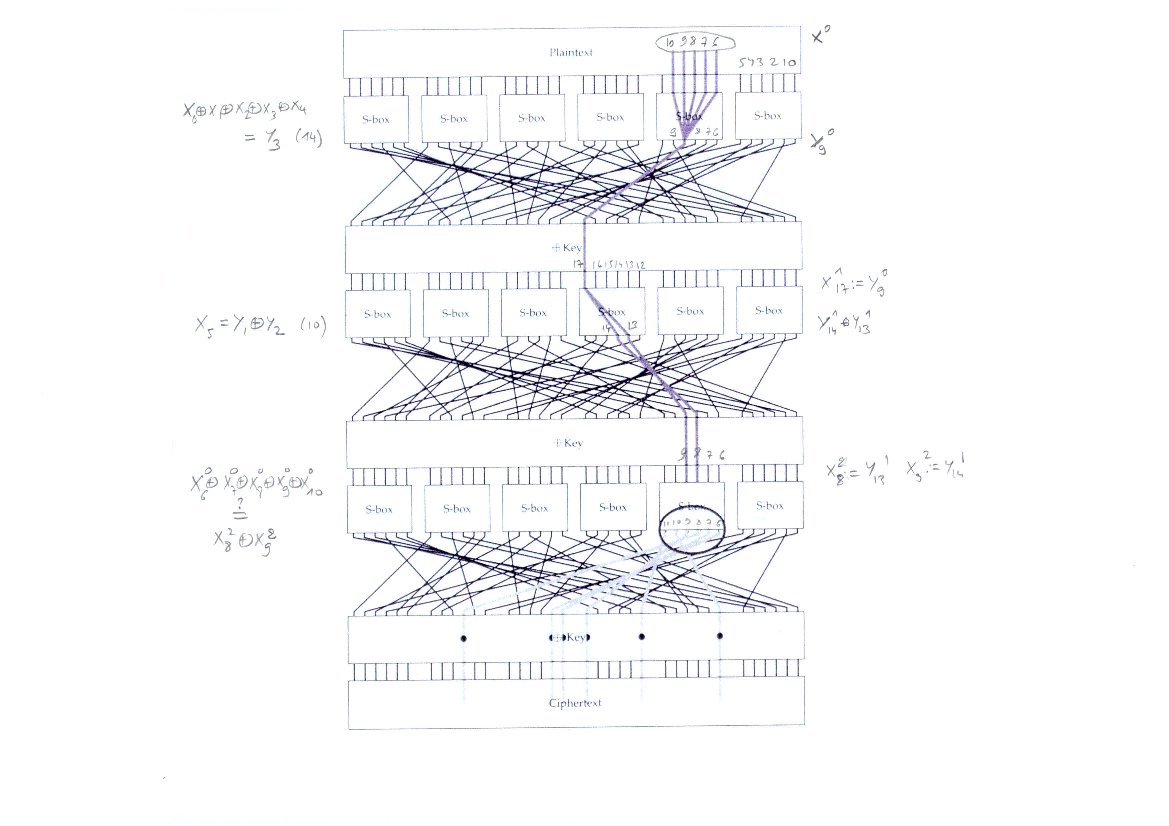
Le programme correspondant (adapté du livre de Swenson) se trouve ici.

Une introduction détaillée à la cryptanalyse linéaire se trouve ici (la plupart des cours qu'on peut trouver sur internet reprennent l'exemple traité dans cet article).