|
|
Compression de Données |
|
Les premiers pas de la compression ont principalement été dirigé vers la compression de données.
En effet, c'est les données qu'on en premier voulu sauvegarder et/ou faire transiter sur des réseaux. |
| Statistique | Le principe d'un algorithme statistique est de parcourir un bloc de données pour détecter les différents motifs qui se répètent en calculant leur fréquence d'apparition. On associe ensuite à chaque motif un symbole qui définit la norme que plus le motif a une grande fréquence et plus le symbole associé a une petite taille. | |||||||||||||||||||||||||||||||||||||||||||||||||||
| retour index | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dictionnaire |
Le principe d'un algorithme par dictionnaire est de remplacer certains termes qui apparaissent plusieurs fois par un symbole bien définit qui sera
stocké dans un dictionnaire. A la décompression, quand on rencontre un nouveau symbole, il suffit de récupérer sa valeur dans le dictionnaire. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| retour index | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Huffman |
Le codage de Huffman, qui date des années 50, repose sur une analyse statistique préalable des données à comprimer. A l'issue de cette analyse,
un arbre est construit qui permet d'attribuer à chaque symbole un code dont le nombre de bits est inversement proportionnel à la probabilité
d'apparition du symbole. Ainsi, les symboles les plus fréquents se voient affecter des codes plus courts, et les codes les plus longs sont attribués
aux symboles rares. En outre, ces codes sont séparables, c'est-à-dire qu'un code donné ne peut pas être le préfixe d'un autre code.
Bien sûr, pour permettre au décodeur de reconnaître les symboles, il est nécessaire de lui transmettre le dictionnaire obtenu après la phase
d'analyse statistique des données.
L'avantage de cet algorithme qui repose sur un type statistique et dictionnaire est qu'il est sans pertes. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| Exemple |
L'on va étudier cet algorithme avec un exemple concret. On va compresser la chaine CASABLANCA.
Une fois que l'on dispose d'un tableau recapitulant les fréquences d'apparition de chaque symbole, il faut reconstruire l'arbre de Huffman. Cet arbre se construit d'après le tableau des fréquences précédents. L'idée est maintenant d'associer les fréquences les plus faibles de tous les caractères.A chaque étape, les deux symboles de plus petite probabilité sont regroupés en un nouveau symbole ayant pour probabilité la somme des deux probabilités. Le processus est itéré jusqu'à obtenir un unique symbole qui sera le père de l'arbre. 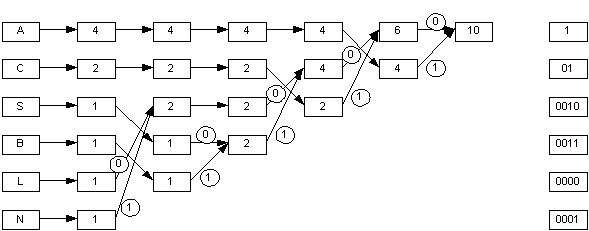
Le code de chaque symbole est ensuite obtenu en suivant le chemin depuis la racine de l'arbre de Huffman jusqu'à la feuille contenant le symbole. Un bit est ajouté à chaque embranchement : 0 si le chemin emprunte la branche supérieure, 1 si c'est la branche inférieure. Ainsi, le code du symbole le plus fréquent (A : 1) est de longueur 1, tandis qu'un symbole rare (N : 0001) est codé sur 4 bits. On arrive donc à des taux de compression assez intéressant à partir du moment ou le fichier est assez gros. En effet, pour que la décompression puisse être réalisée, il faut que le dictionnaire soit transmis. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| retour index | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Lempel Ziv |
L'algorithme de Lempel Ziv repose sur une analyse par dictionnaire. Il parcourt les données et enregistre chaque nouveau symbole en affectant
une nouvelle position dans le dictionnaire. Au début, le dictionnaire contient les 255 du tableau ascii puis sera enrichit au fur et à mesure des
nouveaux symboles rencontrés.
Le gros avantage de cet algorithme, au contraire de celui d'Huffman, est qu'il n'est pas nécessaire de transférer le dictionnaire pour pouvoir décompresser le texte transmis. En effet, le dictionnaire se reconstruit en fonction des nouveaux symboles rencontrés. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| Exemple |
L'algorithme sort : '/WED<256>E<260><261><257>B'. Ici, il ne faut plus que 4*8 + 6*9 = 86 bits. (après /WED, on dépasse 255 : il faut utiliser 9 bits). Des variantes de cette méthode de compression sont utilisées dans les format ZIP, RAR, ARJ, CAB, GIF, PNG, TIFF... C'est une méthode très populaire car: * elle est performante : elle compacte bien toutes sortes de données. * elle n'est pas très difficile à programmer. * elle peut travailler sur des données comme elles arrivent : pas besoin d'analyser toutes les données à l'avance comme avec Huffman. * on peut utiliser des dictionnaires plus ou moins gros en fonction de la mémoire que l'on a. (Avec de petits dictionnaires, on compresse un peu moins bien, mais on compresse plus vite). |
|||||||||||||||||||||||||||||||||||||||||||||||||||
| retour index |
