|
Nicolas Borie
Maître de conférences en Informatique Équipe Combinatoire algébrique et calcul formel Bureau 1B173 Université Gustave Eiffel Bâtiment Copernic, 5 Bd Descartes, 77420 Champs-sur-Marne France E-mail: or |

|
Index | Recherche | Enseignement | Software | Borie Awards | PLaTon
Pictures of root system
Pictures of Type A:
Classical cases:
Appliying the patch from the ticket #4327 of the Sage trac server on your sage system, you could also produce the same pictures.
sage:
RootSystem(["A",2]).weight_space().plot(simple_reflection_hyperplanes=True,
bounding_box=[[-2,2],[-2,2]], simple_coroots=True)
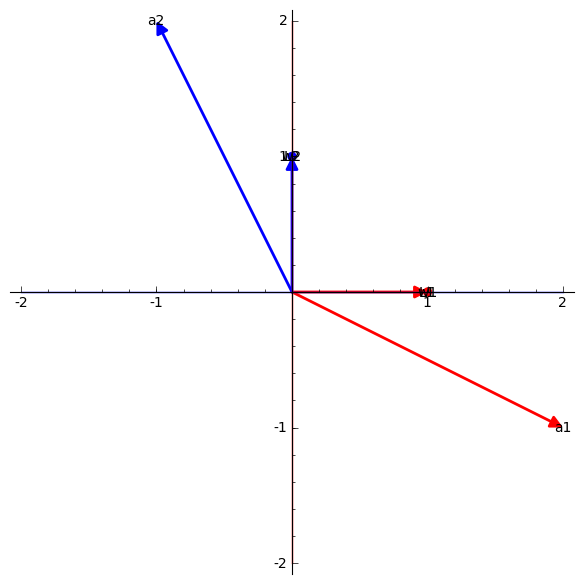
sage:
RootSystem(["A",2]).ambient_space().plot()
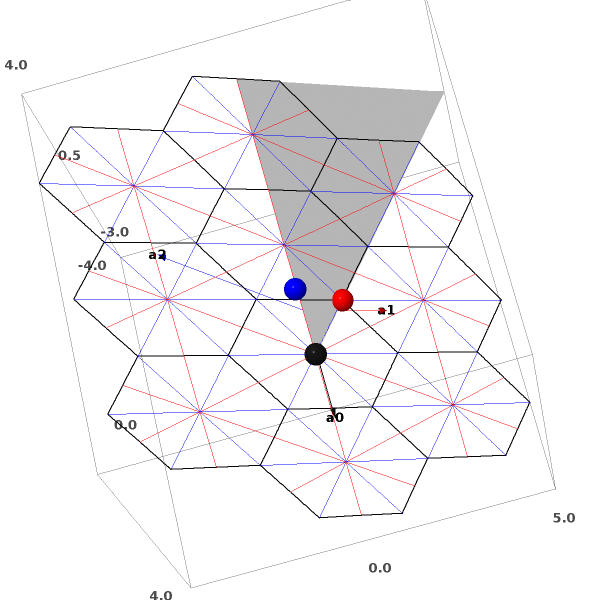
Affine cases:
sage: RootSystem(["A", 2,
1]).weight_space().plot(simple_roots=True, fundamental_weights=True,
alcoves=[[-1..2], [-1..3]],
alcove_walks=[[0,2,1,2,0,2,1,0,2,1,2,1,2,0,2,0,1,2,0],
[2,1,2,0,2,0,2,1,2,0,1,2,1,2,1,0,1,2,0,2,0,1,2,0,2]])
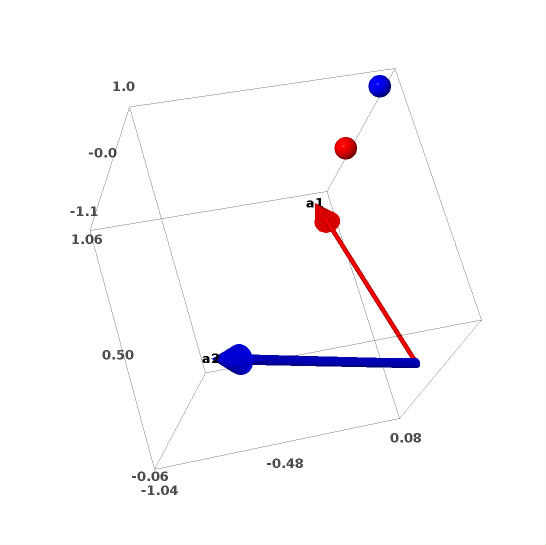
sage: M = matrix(RR,
[[0,1/2,-1/2],[0,sqrt(3)/2,sqrt(3)/2]]); P = RootSystem(["A", 2,
1]).weight_space().plot(alcoves=[[-1..2], [-1..3]], projection =
lambda x : M*vector(RR, x)); P
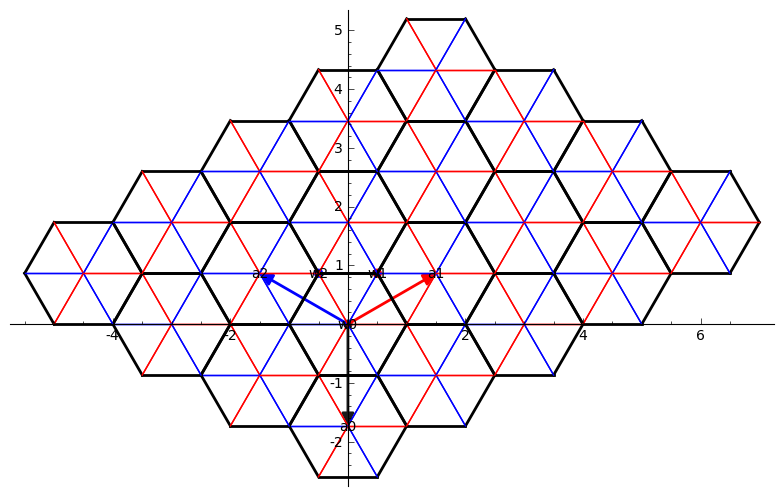
sage: M = matrix(RR,
[[0,sqrt(3)/2,-sqrt(3)/2,0],[0,1/2,1/2,-1],[0,sqrt(2),sqrt(2),sqrt(2)]]);
sage: RootSystem(["A", 3, 1]).weight_space().plot(simple_roots=True, fundamental_weights=True, alcoves=[[0], [0], [0]], projection = lambda x: M*(vector(x)) )
sage: RootSystem(["A", 3, 1]).weight_space().plot(simple_roots=True, fundamental_weights=True, alcoves=[[0], [0], [0]], projection = lambda x: M*(vector(x)) )
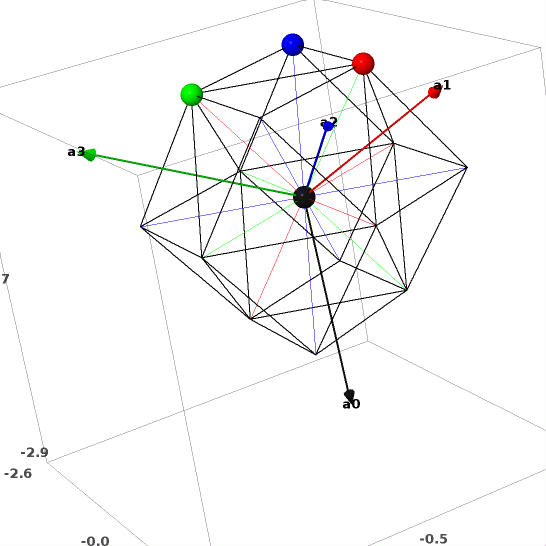
sage: M = matrix(RR,
[[0,1/2,-1/2],[0,sqrt(3)/2,sqrt(3)/2]]); sage: RootSystem(["A", 2,
1]).weight_space().plot(bounding_box=[[-5,5],[-5,5]], projection =
lambda x: M*(vector(x)))
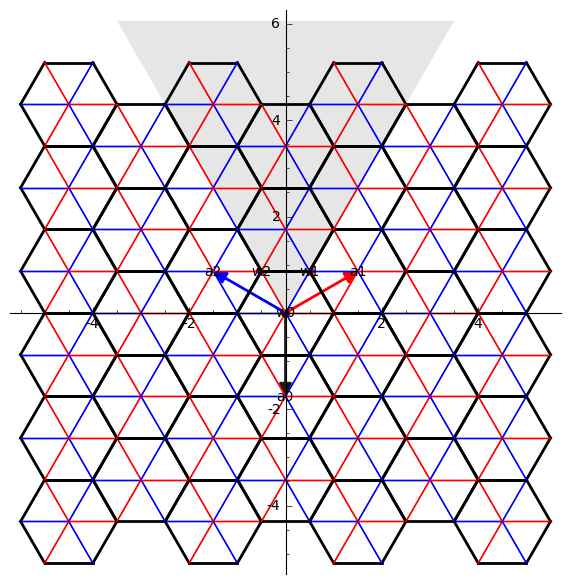
sage: M = matrix(RR, [[0,1/2,-1/2],[0,sqrt(3)/2,sqrt(3)/2]]);
sage: def projection_on_disque(x):
... V = vector(RR, x)
... C = M*V
... d = C.norm()
... return (1-((0.3*d)/(0.3*d+1)))*C
sage: RootSystem(["A", 2, 1]).weight_space().plot(alcoves=[[-4..4],[-4..4]], projection = projection_on_disque)
sage: def projection_on_disque(x):
... V = vector(RR, x)
... C = M*V
... d = C.norm()
... return (1-((0.3*d)/(0.3*d+1)))*C
sage: RootSystem(["A", 2, 1]).weight_space().plot(alcoves=[[-4..4],[-4..4]], projection = projection_on_disque)
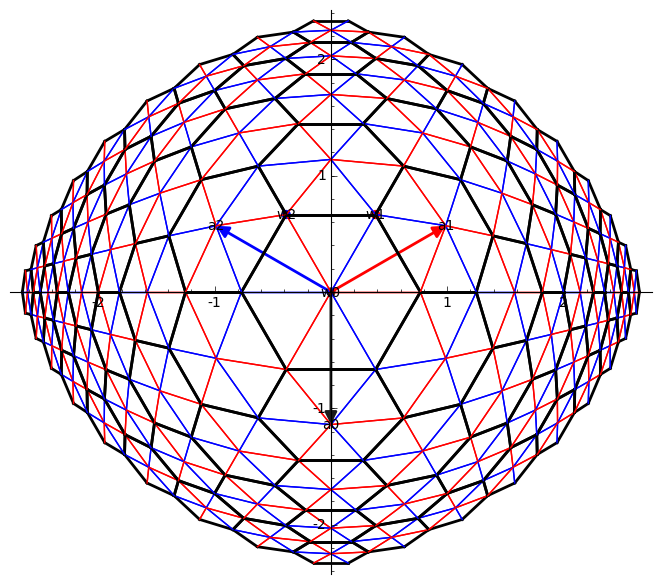
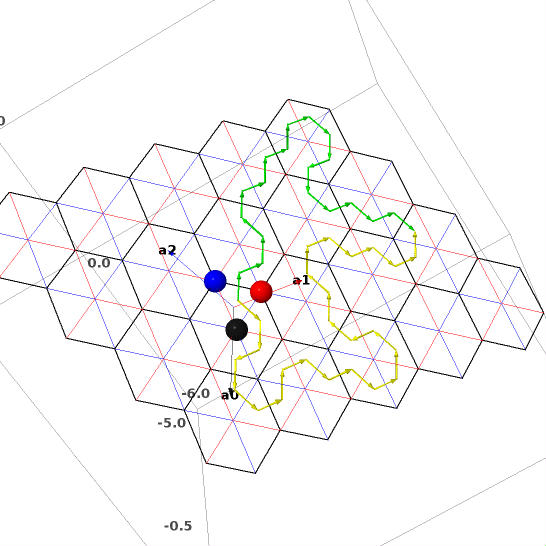
sage: R =
RootSystem(["A",2,1]).weight_space();
sage: W = R.weyl_group();
sage: w0,w1,w2 = W.gens();
sage: w = w0*w2*w1*w0*w1; w.reduced_words()
sage: M = matrix(RR, [[0,1/2,-1/2],[0,sqrt(3)/2,sqrt(3)/2]]);
sage: R.plot(bounding_box=[[-1,2],[0,3]], projection = lambda x: M*(vector(x)), alcove_walks = w.reduced_words())
sage: W = R.weyl_group();
sage: w0,w1,w2 = W.gens();
sage: w = w0*w2*w1*w0*w1; w.reduced_words()
sage: M = matrix(RR, [[0,1/2,-1/2],[0,sqrt(3)/2,sqrt(3)/2]]);
sage: R.plot(bounding_box=[[-1,2],[0,3]], projection = lambda x: M*(vector(x)), alcove_walks = w.reduced_words())
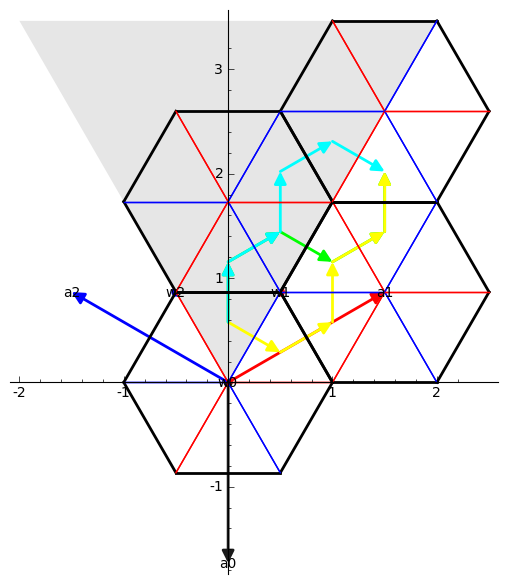
Pictures of Type B or C:
Classical cases:
sage: RootSystem(["B",
2]).ambient_space().plot(simple_coroots=True,
simple_reflection_hyperplanes=True, bounding_box=[[-3,3],
[-3,3]])
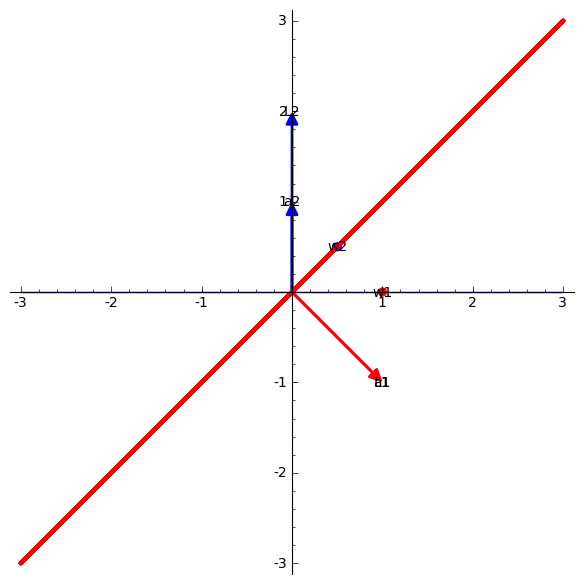
sage: RootSystem(["C",
2]).ambient_space().plot(simple_coroots=True,
simple_reflection_hyperplanes=True, bounding_box=[[-3,3],
[-3,3]])
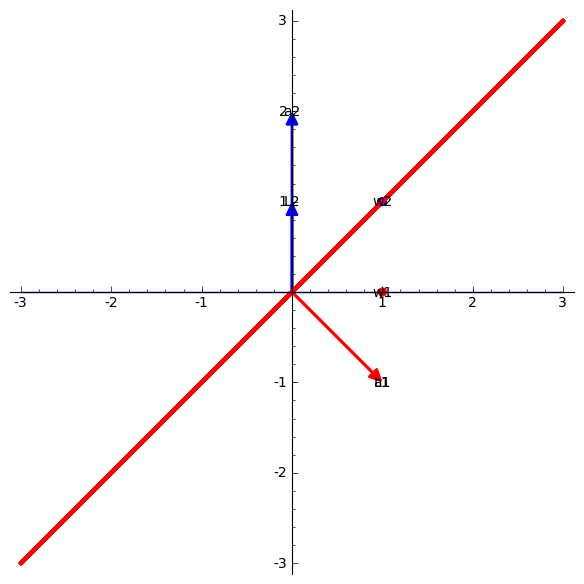
Affine cases:
sage:
RootSystem(["B",2,1]).coweight_space().plot(bounding_box=[[-3,4],[-3,4]],
barycentric=True)
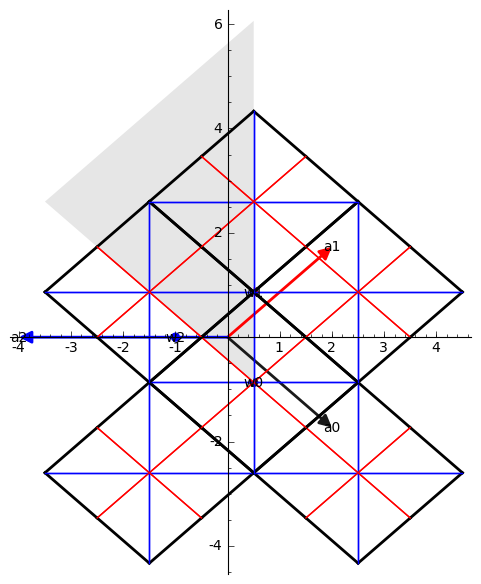
sage: M = Matrix(RR, [[0,1,1],[0,0,1]]); sage:
RootSystem(["C",2,1]).weight_space().plot(bounding_box=[[-3,3],[-3,3]],
projection=lambda x : M*vector(x))
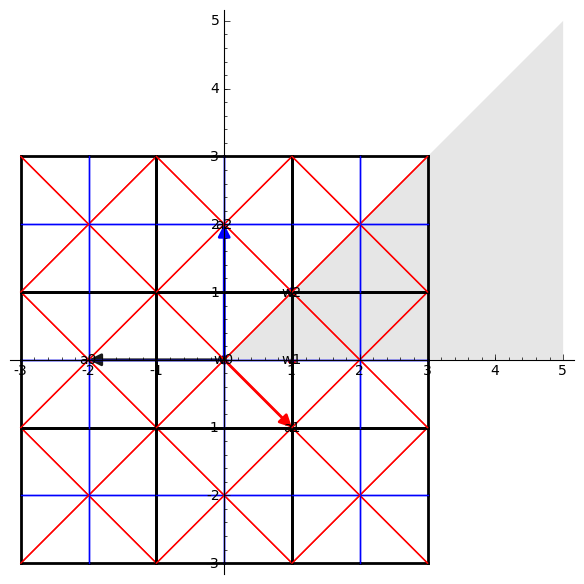
Pictures of Type G:
Classical cases:
sage: RootSystem(["G",
2]).weight_space().plot(simple_coroots=True,
simple_reflection_hyperplanes=True, bounding_box=[[-2,2],
[-2,2]])
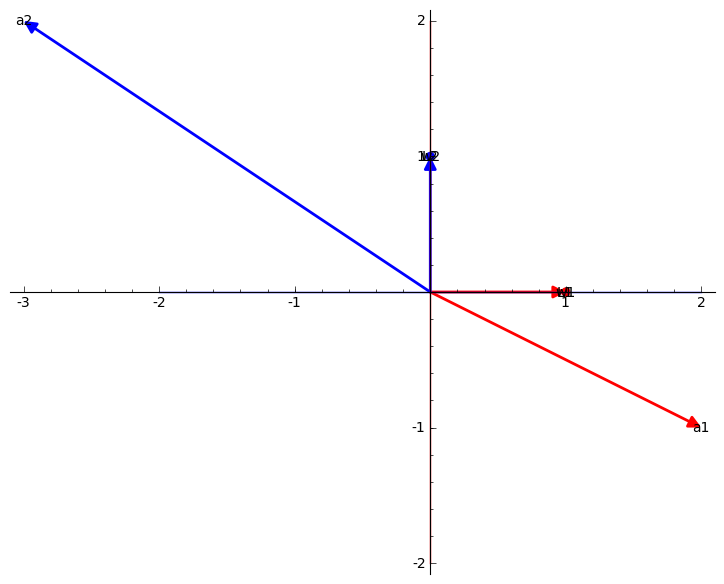
Affine cases:
sage: M = matrix(RR,
[[0,1/2,0],[0,sqrt(3)/2,sqrt(3)]]); sage:
RootSystem(["G",2,1]).weight_space().plot(bounding_box=[[-1,2],[0,4]],
projection = lambda x: M*(vector(x)), alcove_walks =
[[0,2,1,2,0,1]])
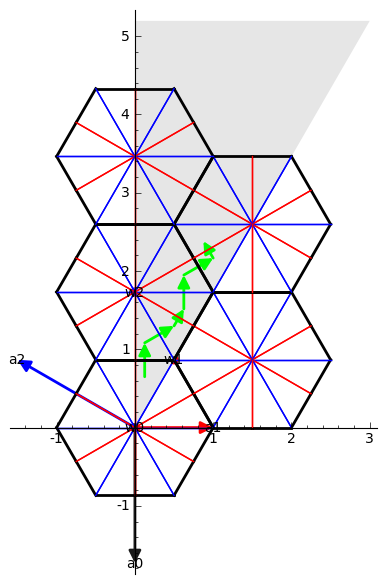
sage:
RootSystem(["G",2,1]).weight_space().plot(bounding_box=[[-3,3],[-3,3],[-3,3]])