Searching a word x with an automaton consists first in building the minimal Deterministic Finite Automaton (DFA) A(x) recognizing the language 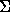 *x.
*x.
- The DFA A(x) =(Q, q0, T, E) recognizing the language
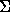 *x is defined as follows:
*x is defined as follows:
-
 |
Q is the set of all the prefixes of x: Q={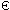 , x[0], x[0 .. 1], ... , x[0 .. m-2], x}; , x[0], x[0 .. 1], ... , x[0 .. m-2], x}; |
-
 |
q0=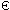 ; ; |
-
 |
T={x}; |
-
 |
for q in Q (q is a prefix of x) and a in 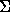 , (q, a, qa) is in E if and only if qa is also a prefix of x, otherwise (q, a, p) is in E such that p is the longest suffix of qa which is a prefix of x. , (q, a, qa) is in E if and only if qa is also a prefix of x, otherwise (q, a, p) is in E such that p is the longest suffix of qa which is a prefix of x. |
The DFA A(x) can be constructed in O(m+ ) time and O(m
) time and O(m ) space.
) space.
Once the DFA A(x) is build, searching for a word x in a text y consists in parsing the text y with the DFA A(x) beginning with the initial state q0. Each time the terminal state is encountered an occurrence of x is reported.
The searching phase can be performed in O(n) time if the automaton is stored in a direct access table, in O(nlog( )) otherwise.
)) otherwise.
void preAut(char *x, int m, Graph aut) {
int i, state, target, oldTarget;
for (state = getInitial(aut), i = 0; i < m; ++i) {
oldTarget = getTarget(aut, state, x[i]);
target = newVertex(aut);
setTarget(aut, state, x[i], target);
copyVertex(aut, target, oldTarget);
state = target;
}
setTerminal(aut, state);
}
void AUT(char *x, int m, char *y, int n) {
int j, state;
Graph aut;
/* Preprocessing */
aut = newAutomaton(m + 1, (m + 1)*ASIZE);
preAut(x, m, aut);
/* Searching */
for (state = getInitial(aut), j = 0; j < n; ++j) {
state = getTarget(aut, state, y[j]);
if (isTerminal(aut, state))
OUTPUT(j - m + 1);
}
}
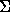 *x;
*x; ) if the automaton is stored in a direct access table;
) if the automaton is stored in a direct access table; ) time complexity;
) time complexity; )) otherwise.
)) otherwise.
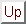



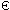 , x[0], x[0 .. 1], ... , x[0 .. m-2], x}
, x[0], x[0 .. 1], ... , x[0 .. m-2], x}