- refinement of the Boyer-Moore algorithm;
- partitions the set of pattern positions into two disjoint subsets;
- preprocessing phase in O(m2) time and O(m
 ) space;
) space; - searching phase in O(n) time complexity;
- 2n text character comparisons in the worst case.

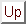


 ) space;
) space;The character comparisons are done using a specific order given by a table h.
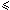 i
i 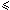 m we define two disjoint sets:
m we define two disjoint sets: |
Pos(i)={k : 0 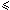 k k 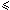 i and x[i] = x[i-k]} i and x[i] = x[i-k]} |
 |
Neg(i)={k : 0 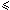 k k 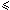 i and x[i] i and x[i] 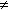 x[i-k]} x[i-k]} |
For 1 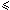 k
k 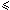 m, let hmin[k] be the minimum integer
m, let hmin[k] be the minimum integer 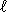 such that
such that 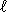
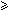 k-1 and k not in Neg(i) for all i such that
k-1 and k not in Neg(i) for all i such that 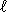 < i
< i 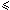 m-1.
m-1.
For 0 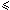
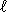
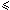 m-1, let kmin[
m-1, let kmin[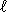 ] be the minimum integer k such that hmin[k]=
] be the minimum integer k such that hmin[k]=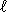
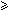 k if any such k exists and kmin[
k if any such k exists and kmin[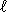 ]=0 otherwise.
]=0 otherwise.
For 0 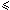
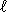
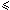 m-1, let rmin[
m-1, let rmin[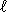 ] be the minimum integer k such that r >
] be the minimum integer k such that r > 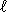 and hmin[r]=r-1.
and hmin[r]=r-1.
The value of h[0] is set to m-1. After that we choose in increasing order of kmin[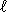 ], all the indexes h[1], ... , h[d] such that kmin[h[i]]
], all the indexes h[1], ... , h[d] such that kmin[h[i]] 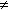 0 and we set rcGs[i] to kmin[h[i]] for 1
0 and we set rcGs[i] to kmin[h[i]] for 1 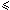 i
i 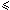 d. Then we choose the indexes h[d+1], ... , h[m-1] in increasing order and we set rcGs[i] to rmin[h[i]] for d < i < m.
d. Then we choose the indexes h[d+1], ... , h[m-1] in increasing order and we set rcGs[i] to rmin[h[i]] for d < i < m.
The value of rcGs[m] is set to the period of x.
The table rcBc is defined as follows: rcBc[a, s]=min{k : (k=m or x[m-k-1]=a) and (k > m-s-1 or x[m-k-s-1]=x[m-s-1])} To compute the table rcBc we define: for each c in 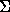 , locc[c] is the index of the rightmost occurrence of c in x[0 .. m-2] (locc[c] is set to -1 if c does not occur in x[0 .. m-2]).
, locc[c] is the index of the rightmost occurrence of c in x[0 .. m-2] (locc[c] is set to -1 if c does not occur in x[0 .. m-2]).
A table link is used to link downward all the occurrences of each pattern character.
The preprocessing phase can be performed in O(m2) time and O(m ) space complexity. The searching phase is in O(n) time complexity.
) space complexity. The searching phase is in O(n) time complexity.
void preRc(char *x, int m, int h[],
int rcBc[ASIZE][XSIZE], int rcGs[]) {
int a, i, j, k, q, r, s,
hmin[XSIZE], kmin[XSIZE], link[XSIZE],
locc[ASIZE], rmin[XSIZE];
/* Computation of link and locc */
for (a = 0; a < ASIZE; ++a)
locc[a] = -1;
link[0] = -1;
for (i = 0; i < m - 1; ++i) {
link[i + 1] = locc[x[i]];
locc[x[i]] = i;
}
/* Computation of rcBc */
for (a = 0; a < ASIZE; ++a)
for (s = 1; s <= m; ++s) {
i = locc[a];
j = link[m - s];
while (i - j != s && j >= 0)
if (i - j > s)
i = link[i + 1];
else
j = link[j + 1];
while (i - j > s)
i = link[i + 1];
rcBc[a][s] = m - i - 1;
}
/* Computation of hmin */
k = 1;
i = m - 1;
while (k <= m) {
while (i - k >= 0 && x[i - k] == x[i])
--i;
hmin[k] = i;
q = k + 1;
while (hmin[q - k] - (q - k) > i) {
hmin[q] = hmin[q - k];
++q;
}
i += (q - k);
k = q;
if (i == m)
i = m - 1;
}
/* Computation of kmin */
memset(kmin, 0, m * sizeof(int));
for (k = m; k > 0; --k)
kmin[hmin[k]] = k;
/* Computation of rmin */
for (i = m - 1; i >= 0; --i) {
if (hmin[i + 1] == i)
r = i + 1;
rmin[i] = r;
}
/* Computation of rcGs */
i = 1;
for (k = 1; k <= m; ++k)
if (hmin[k] != m - 1 && kmin[hmin[k]] == k) {
h[i] = hmin[k];
rcGs[i++] = k;
}
i = m-1;
for (j = m - 2; j >= 0; --j)
if (kmin[j] == 0) {
h[i] = j;
rcGs[i--] = rmin[j];
}
rcGs[m] = rmin[0];
}
void RC(char *x, int m, char *y, int n) {
int i, j, s, rcBc[ASIZE][XSIZE], rcGs[XSIZE], h[XSIZE];
/* Preprocessing */
preRc(x, m, h, rcBc, rcGs);
/* Searching */
j = 0;
s = m;
while (j <= n - m) {
while (j <= n - m && x[m - 1] != y[j + m - 1]) {
s = rcBc[y[j + m - 1]][s];
j += s;
}
for (i = 1; i < m && x[h[i]] == y[j + h[i]]; ++i);
if (i >= m)
OUTPUT(j);
s = rcGs[i];
j += s;
}
}
Preprocessing phase

Tables used by Reverse Colussi algorithm
Searching phase