Expressions arithmétiques

Introduction

Ce Td se compose de deux parties que l'on peut traiter indépendamment. On peut aussi utiliser la première partie pour traiter la seconde. La première partie consiste en la reconnaissance d'expressions arithmétiques formelles. Une expression arithmétique est définie de la façon suivante : ce peut être un terme éventuellement suivi du symbole d'addition + et d'une autre expression. Un terme est défini comme étant un facteur éventuellement suivi du symbole de multiplication * et d'un autre terme. Enfin un facteur peut être un nombre ou un identificateur ou le symbole '(' suivi d'une expression elle-même suivie du symbole ')'. Ces définitions récursives peuvent se schématiser par les règles suivantes :

                E---->T + E / T
                T---->F * T / F
                F---->identificateur / nombre / ( E )

On prendra dans un premier temps comme identificateur les lettres de l'alphabet et comme nombre des chiffres. Ainsi les expressions a+b*c , (x+y)+3 sont correctes. Les expressions +b, (a*b))+c sont syntaxiquement incorrectes.

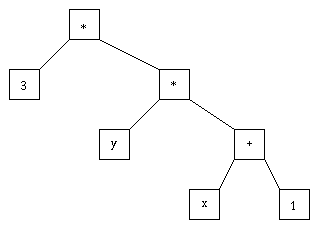
A une expression correcte correspond un arbre syntaxique binaire (car les opérateurs sont binaires). Cet arbre est défini récursivement à partir de la structure de l'expression : l'arbre associé à un identificateur ou un nombre est un noeud formé de cet identificateur ou de ce nombre. L'arbre de ( E ), où E est une expression, est l'arbre de E. L'arbre de T + F est un arbre de racine un noeud contenant le symbole + , de sous arbre gauche l'arbre associé à T et de sous arbre droit l'arbre associé à F (idem pour une expression de type F * T). Par exemple l'arbre syntaxique de 3*(y*(x+1)) est :

La deuxième partie consiste à travailler sur des arbres syntaxiques pour effectuer des dérivations formelles et des simplifications des expressions.

Partie I (difficile)

On pourra commencer par récupérer ici un fichier source à compléter. Le programme comprend une procédure principale qui lit une expression au clavier. On appelle ensuite une fonction Analyse qui vérifie si cette expression est correcte. Cette fonction utilise des fonctions récursives Expression, Terme et Facteur, qui sont à compléter. Chacune cherche à reconnaître une expression, un terme ou un facteur récursivement et renvoie un booléen vrai ou faux indiquant la réussite de la reconnaissance. Le programme comprend une procédure LireLexeme qui fournit dans la variable lex l'unité lexicale suivante. Les unités lexicales possibles sont ici les symboles +, *, (, ), ainsi que les suites de symboles formant un identificateur ou un nombre.

Complétez les fonctions Expression, Terme et Facteur. Le principe de lecture de la variable lex est le même pour les trois fonctions récursives. Décrivons le par exemple pour la fonction Terme. Au moment de l'appel, la variable lex doit toujours contenir la première unité lexicale correspondant au terme que l'on veut reconnaître par l'appel à la fonction Terme. A la sortie de la fonction, la variable lex doit contenir l'unité lexicale qui suit immédiatement le terme en question.
Modifiez les fonctions pour qu'elles calculent l'arbre syntaxique. Vous pourrez faire afficher l'arbre binaire résultat (Td antérieur).

Partie II (plus facile)

On manipule les arbres syntaxiques d'expressions arithmétiques. Les types utilisés peuvent être :

type
        TypeNoeud= (Operateur, Variable, Constante);
	Arbre=^Noeud;
        Noeud= record
                       genre: TypeNoeud;
                       val:char;
                       filsG, filsD : Arbre;
               end;

On supposera que les constantes sont des entiers avec un seul chiffre, que les variables n'ont qu'une seule lettre et que les opérateurs sont +,*,-. On demande d'écrire les procédures suivantes :

Ecrire une fonction d'entête function CreerArbre(genre: TypeNoeud; val:char; g, d: Arbre) : Arbre qui crée l'arbre de racine un noeud du genre TypeNoeud de valeur val, de fils gauche g et de fils droit d.
Ecrire une fonction d'entête function CopierArbre(e: Arbre) : Arbre, qui retourne une copie de l'arbre e avec création de noeuds.
Ecrire une fonction d'entête function Derive(e: Arbre; x: char) : Arbre, qui retourne une copie de l'arbre dérivé de e par rapport à x.

Si vous n'avez pas traité la partie I, les expressions seront rentrées "à la main" comme dans l'exemple ci-dessous. Sinon vous utiliserez les arbres (avec leur type) que vous avez créés en partie I.

var e : Arbre;
begin
   e:= CreerArbre(Constante,'1', nil, nil);
   e:= CreerArbre(Operateur,'+', CreerArbre(Variable,'x', nil, nil),e);
   e:= CreerArbre(Operateur,'*', CreerArbre(Variable,'y', nil, nil),e);
   e:= CreerArbre(Operateur,'*', CreerArbre(Constante,'3', nil, nil),e);
end;

On fera afficher les arbres binaires (Td précédent).

Une solution apparaîtra ici pour la partie II seulement et là pour les parties I et II.

Extensions possibles

On pourra utiliser d'autres opérateurs : /, ^, des fonctions comme L pour log ou E pour exp, etc ... On peut aussi écrire une procédure de simplication d'une expression sur l'arbre syntaxique. S'il vous reste du temps, programmez la simplification d'une expression.

N'oubliez pas de :

m'envoyer votre programme à l'adresse habituelle : beal@monge.univ-mlv.fr.