L'objectif de ce TP est de calculer l'enveloppe convexe d'un ensemble fini de points du plan, c'est-à-dire le contour du plus petit polygone convexe contenant tous les points. La méthode utilisée est celle de Graham. Elle se compose deux parties : le tri des points suivant l'ordre polaire par rapport à une demi-droite (cette partie vous est fournie à l'aide d'un fichier à compléter que vous pouvez récupérer ici), puis le calcul de l'enveloppe à partir de la donnée triée précédente des points (cette deuxième partie est parfois appelée la marche de Graham).

Les points seront entrés en cliquant dans la fenêtre graphique et en terminant la saisie par un double clic sur un point. Les points saisis, au maximum MAX points, seront entrés dans un tableau t du type EnsemblePoint d'éléments de type Point. La fonction EntrePoints effectue cette saisie et renvoie le nombre n de points saisis.
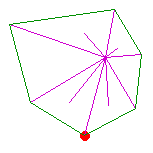
La première étape consiste à choisir un point origine O intérieur à l'enveloppe convexe et un deuxième point p1 dont on est sûr qu'il appartient à cette enveloppe. On prendra par exemple pour p1 le point d'ordonnée maximale et, en cas d'égalité, d'abscisse maximale. (Ce point est représenté plus gros que les autres à l'affichage pour le visualiser).
On effectue ensuite un tri des points suivant l'ordre polaire par rapport à la demi droite définie par l'origine et le point p1. Un point p est avant un autre q pour cet ordre si, en effectuant un balayage dans le sens positif de la demi droite, on trouve p avant q. En cas d'appartenance au même rayon, le plus loin de l'origine est avant l'autre. Il s'agit d'un ordre total sur le plan privé de l'origine. Les points étant stockés dans un tableau, on peut programmer un tri simple ou un quicksort en O(nlog(n)), si n est le nombre de points. Une procédure permettant de tracer les rayons dans l'ordre est donnée. L'affichage se fait rayon par rayon en attendant un clic. Cette partie est déja réalisée.
Les points étant triés comme ci-dessus, le premier point est le point p1 qui est dans l'enveloppe. On range cette suite de points dans une liste doublement chaînée circulaire de points de type ListePoint. Le résulat sera un pointeur l sur le début de la liste. Ainsi si les points sont dans l'ordre p1 p2 ... pn, l pointe sur p1, son successeur pointe sur p2, son prédécesseur pointe sur pn. Une gestion minimale de ces listes doit comprendre
début
t:=debutliste {pointe sur p1 au debut};
Tant que (succ(t) < > debutliste) faire
début
si (t, succ(t), succ(succ(t))) est un tournant à gauche
alors t:= succ(t);
sinon début
supprimer de la liste succ(t);
si (t < > debutliste) alors t:= pred(t);
fin
fin
fin
Un tournant à gauche pour des points p,q,r
est obtenu si r est à gauche de la droite orientée pq.
Vous compléterez la marche de Graham dans la procédure
GrahamScan(var l:ListePoint). La liste l
contient à la fin le contour de l'enveloppe convexe dans l'ordre.
On affiche l'enveloppe convexe par la procédure d'entête
TraceEnveloppe(l:ListePoint).
Une solution apparaîtra ici.
On remarquera que si le tri peut être fait en nlog(n), où n est le nombre de points, la marche de Graham est linéaire. Prouvez le. Montrez aussi pourquoi cet algorithme permet d'obtenir l'enveloppe convexe. S'il vous reste du temps, vous pouvez modifier le programme de façon à afficher l'enveloppe convexe des points restant après l'enlèvement de leur enveloppe, et itérer cette opération : on obtient plusieurs couches d'enveloppes convexes.
