Vous connaissez sans doute tous le code Morse donné par la table ci-dessous. Les messages sont des suites de points, tirets ou blancs (codés ici par le symbole /). Pour décoder un message, on le découpe après chaque blanc et on regarde à quelle lettre correspond le bloc obtenu. Les blancs jouent ainsi le rôle de marqueur de fin de mot de code.
| a | .-/ | j | .---/ | s | .../ |
| b | -.../ | k | -.- | t | -/ |
| c | -.-./ | l | .-../ | u | ..-/ |
| d | -../ | m | --/ | v | ...-/ |
| e | ./ | n | -./ | w | .--/ |
| f | ..-./ | o | ---/ | x | -..-/ |
| g | --./ | p | .--./ | y | -.--/ |
| h | ..../ | q | --.-/ | z | --../ |
| i | ../ | r | .-./ |
Plus généralement, on dit qu'une suite de mots est un code si tout mot admet au plus un découpage en mots du code. Par exemple, les codes de Huffman (voir Td5) sont des codes. L'ensemble {a,ab,ac} est un code. Mais {a,ab,ba} n'en n'est pas un car aba se découpe de deux façons : a puis ab ou ab puis a.
Il n'est pas toujours facile de voir au premier coup d'oeil si une suite de mots est un code. L'ensemble suivant par exemple n'est pas un code : {a,bb,abbba,babab}. En effet le mot abbbabababbba admet les deux décompositions suivantes :
| a | bb | babab | abbba | ||||||||
| abbba | babab | bb | a | |||||||||
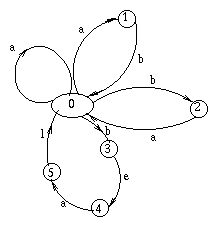
Le problème est néanmoins décidable et on peut procéder de la façon suivante pour le résoudre. On entre les mots au clavier et on construit un graphe représentant ces mots appelé automate en pétales. Ce graphe comporte un état central noté 0 et, pour chaque mot, il existe un chemin d'étiquette ce mot partant de 0 et revenant sur 0. Les états intermédiaires sont tous distincts et chaque flèche comporte un symbole (l'étiquette) indiquant la lettre lue. On note x--a-->y une flèche allant de x vers y et d'étiquette a. L'étiquette du chemin est la suite des étiquettes des flèches. Ainsi à chaque mot correspond un pétale sur le graphe, d'où le nom (voir figure).

type
PtSimple= ^BoiteSimple;
BoiteSimple=record
num: integer;
etiquette :char;
suivant:PtSimple;
end;
Graphe= array[0..NbMax] of PtSimple;
On construit ensuite un nouveau graphe appelé automate des couples obtenu à partir du précedent. Ses sommets
sont les couples de sommets de l'automate en pétales.
Et il existe dans l'automate des couples une flèche :
(x,y)---a---->(z,t) si et seulement si il existe
une flèche x---a--->z et une flèche y---a--->t
dans l'automate en pétales.
Les types pour l'automate des couples seront :
type
PtCouple = ^BoiteCouple;
BoiteCouple = record
num1: integer;
num2: integer;
etiquette: char;
suivant: PtCouple;
end;
Couple = array[0..NbMax, 0..NbMax] of PtCouple;
On remarque maintenant que l'ensemble des mots n'est pas un code
s'il existe dans le graphe simple (l'automate en pétales)
deux chemins distincts de même étiquette
partant de 0 et revenant sur 0. Dans l'automate des couples,
ceci correspond à l'existence
d'un chemin partant de l'état (0,0), passant par un état
(x,y) avec x différent de y, et revenant sur (0,0).
On peut même voir qu'il suffit de montrer qu'il existe
un chemin de (0,0) à un sommet (x,y) (avec x différent de y)
et une flèche de ce sommet (x,y) vers 0.
Dans ce cas on peut mémoriser un tel chemin, ce qui fournit
implicitement une décomposition multiple. Par exemple
pour l'ensemble {a,ab,ba}, on trouvera le chemin :
(0,0)--a-->(0,1)--b-->(2,0)--a-->(0,0).
Si l'on dispose de l'automate des couples, on peut donc tester
si un ensemble de mots est un code en une exploration
du graphe des couples (en largeur ou en profondeur).
Vous pouvez récupérer ici le fichier source à compléter. La saisie des mots est une lecture d'un mot par ligne en terminant par une ligne contenant le symbole '.'. La construction de l'automate en pétales est réalisée. Vous devez compléter la construction del'automate des couples et effectuer un parcours (Trémaux) pour tester si un ensemble de mots est ou non un code.
Une réponse oui ou non à l'exécution n'est pas suffisante pour être sûr que le programme est juste. Dans le cas où l'ensemble de mots n'est pas un code, on affichera un chemin de décompositions multiples. On peut remarquer que les paires (au lieu des couples d'états) suffiraient. Il existe enfin d'autres algorithmes et implémentations plus performants pour résoudre ce problème (voir le projet de tronc commun proposé par J. Berstel aux X93).
Une solution apparaîtra ici.
